Równanie Student: sin2016x−cos2016x=1 , jak rozwiązać takie równanie ?

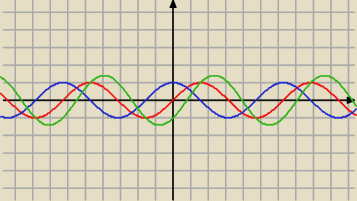
Adamm: widzimy że równanie sinx−cosx=1 ma rozwiązania dla x=π/2+2kπ ∨ x=π+2kπ

Student: Zielony wykres to cała ta funkcja, tak ?

Adamm: tak

Adamm: można też tak sin2016x−cos2016x = sin(2016x)+sin(−π/2−2016x) i teraz wzór na sumę sinusów sin(2016x)+sin(−π/2−2016x)=2sin(−π/4)cos(2016x+π/4)

	√2
cos(2016x+π/4)=−
	2

Student: A mogła bym prosić o dokładne rozpisanie, jak on powstał ?

Student: A z jedynki trygonometrycznej, też by można było to zrobić ?

Adamm: ze wzoru na sumę kątów, trochę się podstawia i jakoś wychodzi

	x+y		x−y
sinx+siny=2sin		cos
	2		2

Adamm: zakładasz że sin(2016x)−cos(2016x)>0 sin(2016x)−cos(2016x)=1 1−2sin(2016x)cos(2016)x=1 sin(2016x)=0 lub cos(2016x)=0

Adamm: tak to można było zrobić za pomocą jedynki

Student: Super, dziękuję bardzo za pomoc