proszę o pomoc studentka: Oblicz długość łuku

	2t
x=
	1+t2

	1−t2
y=
	1+t2

−1≤t≤1

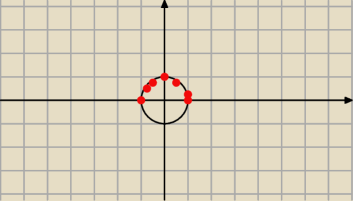
Adamm: t=tg(s/2), −π/4≤s/2≤π/4 ⇔ −π/2≤s≤π/2 x=sin(s) y=cos(s) równanie okręgu o promieniu 1

	1
długość wynosi L=		2π = π
	2

studentka:

	(2t)'(1+t2)−2t(1+t2)'
f'(x)=
	(1+t2)2

	2+2t2−4t2		2−2t2
f'(x)=		=
	1+2t2+t4		1+2t2+t4

	(1−t2)'(1+t2)−(1−t2)(1+t2)'
f'(y)=
	(1+t2)2

	−4t
f'(y)=
	1+2t2+t4

i dalej mam problem

studentka: Adam mógłbyś to szczegółowo opisać bo ja liczyłam ze wzoru na długość krzywej

Adamm:

	2(1+t2)−2t*2t		2(1−t2)
x'=		=
	(1+t2)2		(1+t2)2

	−2t(1+t2)−2t(1−t2)		−4t
y'=		=
	(1+t2)2		(1+t2)2

	√4(1−t2)2+16t2		2
∫−11		dt = 2∫01		dt = 4arctg1 = π
	(1+t2)2		1+t2

Adamm: tak to można było zrobić całką

studentka: Ale chyba zapomniałeś o 1+ we wzorze ?

Adamm: o niczym nie zapomniałem

studentka: √1+[f'(x)]²

Adamm:

	dx		dy
można powiedzieć że korzystałem z "rozszerzenia" tego wzoru √(		)2+(		)2
	dt		dt

Adamm: to nie jest zwykła funkcja tylko funkcja w postaci parametrycznej można byłoby spróbować sprowadzić ją do funkcji y=√1−x², −1≤x≤1

studentka: to jeszcze ostatnie pytanie czemu w ostatniej całce granica całkowania to 0 a nie −1 ?

Adamm: jeśli funkcja f jest parzysta to ∫_−a^a f(x) dx = 2∫₀^a f(x) dx

studentka: Dziękuję, będziesz jeszcze potem bo mam jedno zadanko z którym mam problem

Adamm: jeśli popatrzysz na interpretację geometryczną całki to to co powiedziałem 15:59 zdaje się oczywiste

Adamm: nie wiem, może będę

Mariusz:

	2t
x=
	1+t2

	1−t2
y=
	1+t2

	2(1+t2)−2t*2t		1−t2
x'=		=2
	(1+t2)2		(1+t2)2

	−2t(1+t2)−2t(1−t2)		4t
y'=		=−
	(1+t2)2		(1+t2)2

	4(1−t2)2		16t2
(x')2+(y')2=		+
	(1+t2)4		(1+t2)4

	1−2t2+t4		4t2
=4(		+		dt
	(1+t2)4		(1+t2)4

	(1+t2)2
=4
	(1+t2)4

	1
=4
	(1+t2)2

	1
∫−112		dt
	1+t2

=2arctan(t)|₋₁¹ =2arctan(1)−2arctan(−1)

	π		π		π		π
=		−(−		)=		+
	2		2		2		2

=π