równanie wartość: |2x²−3|−|x²−1|=2 Rozwiąż

Jack: przedzialy i jedziem

===: nie za dużo tych przedziałów

relaa: Chyba, że tak zrobić. |2x² − 3| − |x² − 1| = 2 |2x² − 3| = |x² − 1| + 2 2x² − 3 = |x² − 1| + 2 ∨ 2x² − 3 = −|x² − 1| − 2 |x² − 1| = 2x² − 5 ∨ |x² − 1| = 1 − 2x² Dla x ∊ (−1 ; 1) −(x² − 1) = 2x² − 5 ∨ −(x² − 1) = 1 − 2x² x² = 2 ∨ x² = 0 x = ±√2 ∨ x = 0 ⇒ x = 0 dla x ∊ (−∞ ; −1] ∪ [1 ; ∞) x² − 1 = 2x² − 5 ∨ x² − 1 = 1 − 2x²

	2
x2 = 4 ∨ x2 =
	3

	√2
x = ±2 ∨ x = ±		⇒ x = ±2
	√3

x ∊ {−2 ; 0 ; 2}

wartość: Ojeju, nie mam pojęcia co Tu się stało nawet, ale wyniki poprawne

Jack: |x| = |y| x = − |y| lub x = |y| wiec |x| = |y| + a x = −(|y|+a) lub x = |y|+a x = −|y| − a lub x = |y|+a i potem analogicznie

yht: to nic trudnego wyznaczasz jedną wartość bezwzględną, np. |2x²−3| |2x²−3| = |x²−1|+2 za prawą stronę równania podstawiasz t, czyli |x²−1|+2 = t |2x²−3| = t rozbijasz wart bezwzgl na zasadzie że jeśli |coś|=2 to coś=2 lub coś=−2 2x²−3=t ∨ 2x²−3=−t wracasz do poprzedniej zmiennej 2x²−3=|x²−1|+2 ∨ 2x²−3=−(|x²−1|+2) 2x²−3−2=|x²−1| ∨ 2x²−3=−|x²−1|−2 2x²−5=|x²−1| ∨ |x²−1|=−2+3−2x² |x²−1|=2x²−5 ∨ |x²−1|=1−2x² dalej podobnie jak na początku, 2x²−5=t, 1−2x²=u |x²−1|=t ∨ |x²−1|=u x²−1=t ∨ x²−1=−t ∨ x²−1=u ∨ x²−1=−u wracasz do iksa rozwiązujesz 4 równania kwadratowe wychodzi ci zbiór (podejrzanych) rozwiązań równania wyjściowego czyli |2x²−3| = |x²−1|+2 wstawiasz za x kolejno każdą z liczb ze zbioru rozwiązań podejrzanych do równania |2x²−3| = |x²−1|+2 tylko ten x który po wstawieniu do równania |2x²−3| = |x²−1|+2 daje równość prawdziwą, jest rozwiązaniem równania |2x²−3| = |x²−1|+2

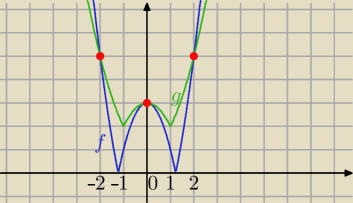
Mila: Graficznie: f(x)=|2x²−3| g(x)=|x²−1|+2 szkicuję wykresy ( są proste do narysowania) Z obserwacji: 3 rozwiązania x=0 lub x=2 lub x=−2 sprawdzam równanie |2x²−3|−|x²−1|=2 x=0 L=|−3|−|−1|=3−1=2=P x=−2 L=|2*4−3|−|4−1|=|5|−|3|=2=P x=2 L=P odp. x∊{0,−2,2}

dobra wartość: wartość nadal nie wie co tu się dzieje ale najważniejsze sa dobre wyniki bo za nie dają punkty

Mila: To masz problem, spróbuj analizować i zadawać pytania. Dobrego wyniku na testach nie uzyskasz, jeśli nie rozwiążesz. A to może zadanie zamknięte było?