Na płaszczyźnie zespolonej narysować zbiór liczb z spełniających podane warunki:
MaTT: Na płaszczyźnie zespolonej narysować zbiór liczb z spełniających podane warunki:
a) {z ε ℂ: Re(z−i)
2≥0}
Tutaj próbowałem coś liczyć i otrzymałem a
2−(b−1)
2≥1, prosze o potwierdzenie, bądź
zaprzeczenie.
| | π | |
b){z ε ℂ: 0<arg(iz)< |
| } |
| | 4 | |
c){z ε ℂ: z=2−3i+2e
it, t ε ℛ}
16 gru 15:03
Jerzy:
a) x2 − (y −1)2 ≥ 0 ⇔ (x + y − 1)(x − y +1) ≥0
16 gru 15:26
MaTT: A co dalej?
16 gru 15:57
Adamm:
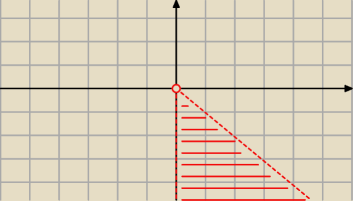
b) z≠0, zauważ że mnożenie przez i jest obróceniem płaszczyzny o 90
o lub inaczej π/2
0<arg(iz)<π/4 ⇔ −π/2<arg(z)<−π/4
16 gru 16:55
MaTT: A jak zabrać się za podpunkt c?
16 gru 17:01
Adamm:
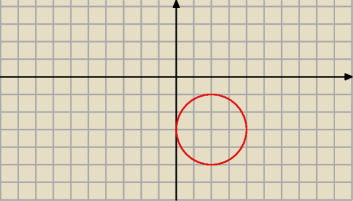
e
it jest okręgiem o promieniu 1, 2−3i+2e
it jest okręgiem o promieniu 2 o środku (2; −3)
16 gru 17:09