zadanie
Sławek: pomocyy
rozwiąż równania
a) 4x+2 = 256
16 gru 09:49
5-latek: Na czym polega ta trudnosc (konkretnie .
16 gru 09:52
Jerzy:
Na braku elementarnej wiedzy z potęgowania
Witaj
małolat
16 gru 09:59
5-latek: Witam
Jerzy
Biore sie teraz za przystawanie trojkatow .
Sławek wiola
Masz wzor a
p*a
q= a
p+q (dziala on w obie strony
np 4
x+2 = 4
x*4
2= 4
x*16
A jak masz 4
x*4
2= 4
x+2
Proste ? pewnie ze tak
16 gru 10:03
Mika: Witam,
Czy mógłby ktoś mi podpowiedzieć jak to rozwiązać?
tgα=√3/2
cosα=?
16 gru 11:17
Jerzy:
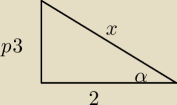
x =
√(√3)2 + 22 =
√3 + 4 =
√7
| | 2 | | 2 | | 2√7 | |
cosα = |
| = |
| = |
| |
| | x | | √7 | | 7 | |
16 gru 11:26
Mika: Dziękuję bardzo
A jak obliczyć (𝑙𝑜𝑔
6 2 + 𝑙𝑜𝑔
6 18)
2
16 gru 11:40
Janek191:
= ( log6 2*18)2 = ( log6 36)2 = 22 = 4
16 gru 11:43
Mika: log5 4 − 𝑙𝑜𝑔5 500
16 gru 11:52
Jerzy:
| | 1 | |
= log5 |
| = log5125−3 = −3log5125 = −3*3 = −9 |
| | 125 | |
16 gru 11:54
Jerzy:
| | 1 | |
Pomyłka ... = log5 |
| = log5125−1 = −1*log553 = −3*log55 = −3*1 = −3 |
| | 125 | |
16 gru 11:56
Mika: Narysuj wykres funkcji wykładniczej f(x)= 2x+1−2 oraz określ jej własności
16 gru 12:04
relaa:
| | 2√7 | |
Czemu nie rozpatrujemy przypadku kiedy cos(α) = − |
| ? |
| | 7 | |
| | 1 | | 1 | |
Jest gotowy wzór cos2(x) = |
| ⇒ cos(x) = ± |
| |
| | tg2(x) + 1 | | √tg2(x) + 1 | |
16 gru 12:06
Jerzy:
Masz rację .. .nie wiem dlaczego założyłem,że : α jest kątem ostrym.
16 gru 12:10
Mika: Zapomniałam dodać w zadaniu jest tangens kąta ostrego
16 gru 12:27
5-latek: To juz wiesz ze tangens jest dodatni w 1 i 3 cwiartce .
16 gru 12:30
Mika: W ostrosłupie prawidłowym czworokątnym kąt nachylenia ściany bocznej do podstawy wynosi 60° .
Oblicz objętość ostrosłupa jeżeli wysokość ostrosłupa ma długość 8 cm.
Objętość wyszła mi 227,55 zaś dł podstawy 16√3/3. Czy dobrze to obliczyłam?
16 gru 12:42
Mila:
4x+2 = 256
4x+2=16*16
4x+2=44
x+2=4
x=2
||
4x+2=256
4x*42=256
4x*16=256 /:16
4x=16
4x=42
x=2
17 gru 18:03
Mila:
12:42 Dobrze.
Objętość podaj w ułamku.
17 gru 18:11