Odległość środka AB od początku układu
Karol: 1.Oblicz odległość środka odcinka AB od początku układu współrzędnych.
A(9,√7) B(−4,−√7)
2. Dany jest punkt A(−4,−3). Oblicz odległość AB, jeśli jego środek leży na osi O X, a odcięta
punktu B jest równa 2.
3. Punkty A(2,−4) i C (−1,−1) są wierzchołkami rombu ABCD. UZasadnij że przekątna BD tego rombu
jest zawarta w prostej x−y−3=0
4. Pole rombu ABCD jest równe 32. Wyznacz współrzędne punktów B i D jeśli A(2,3) C(4,1)
15 gru 21:50
15 gru 22:34
Janek191:
d = √ 2,52 + 02 = 2,5
====================
15 gru 22:36
Eta:
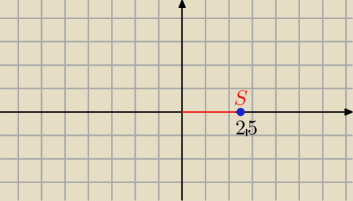
15 gru 22:36
Eta:
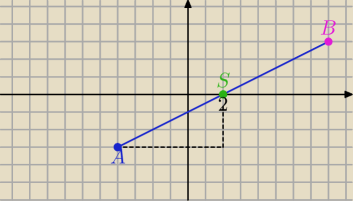
2/ |AS|=
√62+32= ..... |AB|=2|AS|=...
15 gru 22:39
Janek191:
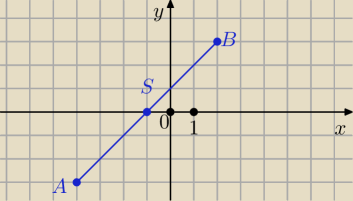
z.2
A = ( − 4, −3)
S = ( x, 0)
B = ( 2, y)
więc
dlatego
B = ( 2, 3)
S = ( − 1, 0)
Pewnie chodzi o długość AB ?
I AB I =
√( 2 − (−4))2 + ( 3 − (−3))2 =
√62 + 62 =
√36*2 = 6
√2
15 gru 22:42
Eta:
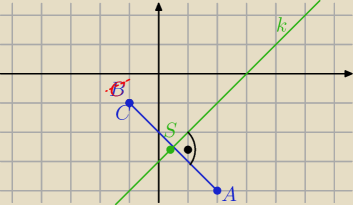
3/ prosta k zawierająca przekątną BD jest prostopadła do prostej AC i przechodzi przez S
| | −1+4 | |
aAC= |
| = −1 to ak = 1 |
| | −1−2 | |
k: y= 1(x−x
S)+y
S ⇒ .................
BD : x−y−3=0
15 gru 22:47
Eta:
Idę spać ...... "baw się dobrze"
Janek 
Dobranoc

15 gru 22:49
Janek191:

16 gru 11:40

 2/ |AS|=√62+32= ..... |AB|=2|AS|=...
2/ |AS|=√62+32= ..... |AB|=2|AS|=...
 z.2
A = ( − 4, −3)
S = ( x, 0)
B = ( 2, y)
więc
z.2
A = ( − 4, −3)
S = ( x, 0)
B = ( 2, y)
więc
 3/ prosta k zawierająca przekątną BD jest prostopadła do prostej AC i przechodzi przez S
3/ prosta k zawierająca przekątną BD jest prostopadła do prostej AC i przechodzi przez S
 Dobranoc
Dobranoc 
