Przyrównywanie ułamka do 0 Kamil: Witam W jaki sposób można przyrównywać ułamki (funkcje wymierne) do 0? Mam na myśli sytuacje w ktorych nie jestem pewny co do mianownika.

2x(x2−9)(x2 + 27)
(x2 −9)4

W tej sytuacji wiem że mianownik jest dodatni, mogę pomnożyć przez niego i liczyć miejsce zerowe góry, ale co powinienem zrobic w takiej sytuacji:

2x(x2 + 27)
(x2 −9)3

Janek191: Mianownik musi być ≠ 0 ⇒ x ≠ −3 i x ≠ 3

Kamil: Ale chodzi mi o to, jak policzyć miejsce zerowe tejfunkcji, tj dla jakich x cały ułamek będzie równy 0

Janek191: Trzeba licznik przyrównać do 0 .

Janek191: licznik = 0 ⇔ x = 0 lub x = − 3 lub x = 3 Odrzucamy x = − 3 i x = 3, bo nie należą do dziedziny Miejsce zerowe : x = 0 ( x² + 27 > 0 dla dowolnego x ∊ ℛ )

Mila: a)

2x*(x2−9)(x2 + 27)
	=0
(x2−9)4

1)mianownik różny od zera x²−9≠0⇔x≠3 i x≠−3 2) Ułamek może mieć wartość 0, jeżeli: 2x(x²−9)(x² + 27) =0 i x≠3 i x≠−3⇔ x=0 ====== b)

2x(x2 + 27)
	=0
(x2−9)3

1) x²−9≠0⇔x≠3 i x≠−3 Ułamek może mieć wartość 0, jeżeli: x(x² + 27) =0 i x≠3 i x≠−3⇔ x=0 ( bo x²+27>0 dla każdego x∊R)

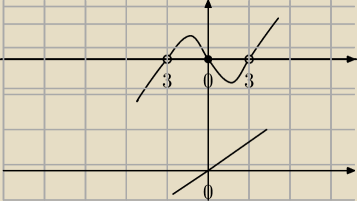
Kamil: Może trochę źle sformułowałem pytanie, mianowicie przed chwilą wpadłem w pewną pułapkę ... Oczywiście że miejscem zerowym jest 0 w obydwu ułamkach, chodzi mi o to że później muszę narysować wykres tej funkcji Drugi ułamek jest pierwszym po skróceniu Tylko że z racji że w pierwszym mianownik jest dodatni, to mnożę przez niego obustronnie i rysuję wykres samej góry który przechodzi przez 3 miejsca zerowe (trójki nie należą do dziedziny) Gdy pomnożę przez mianownik drugi ułamek i narysuje wykres góry otrzymam zupełnie inny wykres, ktory jest niepoprawny Jak sobie radzić z ulamkami z ujemnym mianownikiem?

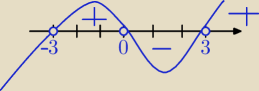
Mila: Bardzo to zaplątałeś, jakie zadanie masz do rozwiązania? Jeżeli nierówność:

2x*(x2−9)(x2 + 27)
	>0⇔ możemy zbadać znak iloczynu
(x2−9)4

( ta sama zasada ustalenia znaku) 2x*((x²−9)*(x²+27)*(x²−9)⁴>0 x*(x²−9)⁵*(x²+27)>0⇔ x*(x²−9)⁵>0 x=0, x=3 (pięciokrotny), x=−3 (pięciokrotny) II przypadek , uprościłeś i masz :

2x*(x2 + 27)
	>0 znów badamy znak iloczynu
(x2−9)3

x*(x²+27)*(x²−9)³>0⇔ x*(x²−9)³>0 i masz to samo rozwiązanie x=0, x=3 (trzykrotny), x=−3 (trzykrotny)

Kamil: Liczę punkty przegięcia funkcji, i muszę narysować wykres A w jaki sposób ułamek z mianownika znalazł się w liczniku?

Mila: Zamiast badać znak ilorazu możesz badać znak iloczynu, jest ta sama zasada ustalenia znaku.

−2
	<0
3

(−2)*3<0

−4
	>0
−9

(−4)*(−9)>0