pochodna
oll: wyznacz ekstrema lokalne funkcji f(x)= |x|−x2
f'(x)= 1−2x dla x>0 i f'(x)= −1−2x dla x<0, f'(x)= −2x dla x=0
co teraz zrobic?
14 gru 22:02
Jack:
f(x) = |x| − x2
dla x < 0 f(x) = − x − x2
dla x ≥ 0 f(x) = x − x2
i teraz dwie pochodne przyrownujemy do zera itd.
przy czym x=0 na pewno nie bedzie ekstremum
14 gru 22:06
Adamm: jesteś pewien
Jack 
kiedy może istnieć ekstremum
14 gru 22:07
Jack:
f(−x) = f(x) zatem wlasciwie... wystarczy rozpatrzec 1 przypadek.
14 gru 22:09
Adamm: pytałem o coś...
14 gru 22:10
Jack: nie mamy pochodnej w zerze ale ekstremum np. dla funkcji |x| istnieje
14 gru 22:11
Adamm:
no właśnie
ekstremum może istnieć w dwóch przypadkach
1. f'(x)=0
2. pochodna nie istnieje
i tu mamy ten drugi, a tak się składa że x=0 jest minimum tej funkcji
14 gru 22:13
Jack: akurat tutaj watpie w istnienie minima...
14 gru 22:15
Adamm: wątpisz w rzeczywistość?
14 gru 22:18
Adamm: ekstremum to punkt dla którego każdy inny punkt w otoczeniu tego punktu jest od niego mniejszy
lub większy
x=0 spełnia definicję tak samo jak x=1/2 czy x=−1/2
14 gru 22:23
14 gru 22:25
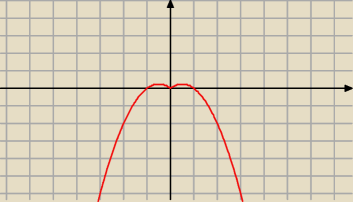
Adamm: najlepiej z rysunku
zauważ że ta funkcja to tylko dwie scalone ze sobą parabole, funkcja jest malejącą dla
x∊<−1/2;0> i rosnąca dla x∊<0;1/2>, teraz to chyba oczywiste
14 gru 22:28
oll: sory ze pewnie pytam o oczywiste rzeczy ale skąd wiem, że jest malejąca lub rosnąca dla tych
przedziałów które podales?
14 gru 22:30
Adamm: a to że x=0 jest ekstremum to też można było zrobić pochodnymi
14 gru 22:30
oll: to jak z pochodnych dowiedziec sie ze x=0?
14 gru 22:31
Adamm: np. z pochodnej
albo przez te wmawiane przez oświatę przesądzenie że parabola to ósmy cud świata
14 gru 22:31
Adamm: masz f'(x)<0 dla x∊(−1/2;0) oraz f'(x)>0 dla x∊(0;1/2)
14 gru 22:32
Adamm: tak samo jak badasz czy gdzieś nie masz minimum dla f'(x)=0, tylko tutaj dobrze byłoby się
powołać na ciągłość funkcji w punkcie x=0
14 gru 22:34
Adamm: bo przecież gdyby na przykład mielibyśmy tą samą funkcję tylko zamiast f(0)=0 mielibyśmy
f(0)=0,001 to by tam nie było ekstremum
14 gru 22:37
oll: napisales masz f'(x)<0 dla x∊(−1/2;0) a na twoim wykresie jest wieksze od zera
14 gru 22:37
Adamm: pochodna
14 gru 22:38
Adamm: to jest wykres funkcji
14 gru 22:38
Adamm: tej pierwotnej
14 gru 22:38
oll: acha, a narysowałbys wykres pochodnej?
14 gru 22:40