Granica jednostronna. Piotr: Witam, mam pewien problem ze zrozumieniem granicy jednostronnej. Mam takie zadanie. Oblicz granice jednostronne funkcji w podanych punktach. Dla przykładu w punkcie x₀=−1

	x2−2		−1
To na początek liczę granice prawostronną: limx→−1+		=[		]
	x2−2x−3		0−

Teraz przedstawię mój tok myślenia i chciałbym się dowiedzieć co w nim jest nie tak. Jeśli zmierzam do −1 z prawej strony, to z prawej strony są wartości większe niż −1. Dla

	9
ułatwienia podstawiam sobie np. −		to w mianowniku będzie wyglądać to tak:
	10

0.81+1,8−3= −0,39 Czyli mianownik zbiega do zera z lewej strony[0⁻]. W liczniku była wartość ujemna. Więc według powinno wyjść ∞ a jest −∞.

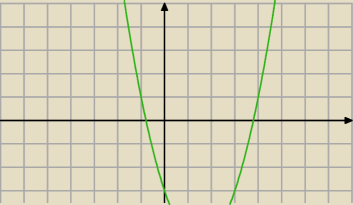
Jerzy: Mianownik nie zmierza do 0

Benny: Jak nie? Przecież −1 jest pierwiastkiem mianownika.

Jerzy:

	2
Weź taką granicę: limx→1+
	x2 − 1

Teraz zauważ,że jak x zmierza do 1 z prawej strony, to po wartościach dodatnich, a więc lim = +∞ Jeśli zmierza z lewej , to po warosciach ujemnych i lim = −∞

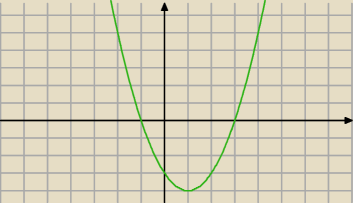
Jerzy: Zle spojrzałem ... teraz jak x → −1 z prawej, to po wartościach ujemnych, a jak z lewej to po dodanich.

Adamm: x²−2x−3=(x+1)(x−3)

	x2−2		−1
limx→−1+		= [		] = ∞
	(x+1)(x−3)		0+*(−4)

Piotr: Czyli w granicy prawostronnej wychodzi ∞, tak? W takim razie mam błąd w książce