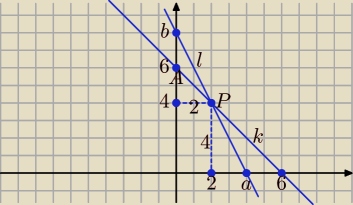
Elementy geometrii analitycznej Matglo: Dana jest prosta k: y = –x + 6, która przecina oś OY w punkcie A. Przez punkt P(2, 4) poprowadzono prostą l, która przecięła oś OY powyżej punktu A. Suma pól dwóch trójkątów powstałych między prostymi k, l oraz osiami układu współrzędnych jest równa 6. Napisz równanie prostej l.

Bogdan:

1		1		b − 4		4
	*4*(6 − a) +		*2*(b − 6) = 6 ⇒ b = 2a i		=
2		2		2		a − 2

2a − 4		4
	=		⇒ a = 4 i b = 8
2		a − 2

	x		y
Korzystając z postaci odcinkowej prostej otrzymujemy równanie prostej l:		+		= 1
	a		b