przebieg zmienności funkcji
madzia: Muszę zbadać przebieg zmienności takiej funkcji:
f(x) = 2x/ex oraz sporządzić jej wykres. Chciałoby się to komuś zrobić krok po kroku,
tak by ktoś z 1 roku studiów po maturze podstawowej to zrozumiał?
13 gru 20:23
Janek191:
Jak musisz, to badaj
13 gru 20:24
Jerzy:
Zacznijmy od dziedziny i pochodnej. Co potrafisz ?
13 gru 20:24
madzia: Dziedzina to liczby rzeczywiste, pochodną z tego też potrafię policzyć, zgubiłam się na
wyznaczaniu asymptot.
13 gru 20:26
madzia: Wiem także, że przecina ona oś w punkcie (0,0).
13 gru 20:27
Jerzy:
Zacznij od ekstremów lokalnych... to już daje pewien pogląd na przebieg funkcji.
13 gru 20:28
madzia: Zaczęłam liczyć granice obustrone, wyszło, że dążą do nieskończoności.
13 gru 20:29
Janek191:
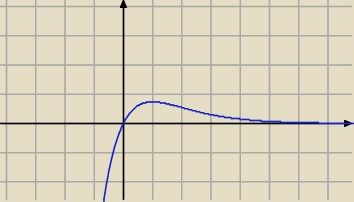
13 gru 20:29
Adamm: asymptota prawostronna y=0 i tyle
13 gru 20:30
madzia: Czyli nie dążą do nieskończoności
13 gru 20:30
madzia: Dobrze, czyli teraz pochodna?
13 gru 20:31
Adamm: ta z lewej nie, do minus nieskończoności
13 gru 20:31
madzia: No tak, tak o to mi chodziło
13 gru 20:31
Jerzy:
Szukaj ekstremum lokalnego.
13 gru 20:33
madzia: Pochodna z tego to:
f'(x) = (2ex − 2xex)/e2x = 2−2x/ex po wyciągnięciu ex przed nawias.
13 gru 20:36
Jerzy:
Kiedy się zeruje ?
13 gru 20:37
madzia: 2−2x/ex = 0
2−2x = 0
x = 1 <−−− czy to jest ekstremum lokalne?
13 gru 20:37
Janek191:
Nawias jest potrzebny
13 gru 20:38
Jerzy:
Musisz sprawdzić, czy pochodna zmienia znak w punkcie x = 1, a jeśli tak, to jak.
13 gru 20:38
Adamm: zmienia, z dodatniego na ujemny, czyli mamy minimum
13 gru 20:39
Jerzy:
@madzia ... wiesz dlaczego tak zmienia znak ?
13 gru 20:40
Janek191:
Maksimum
Patrz na wykres funkcji f.
13 gru 20:40
madzia: No tak, widzę to na wykresie, ale jak to sprawdzić obliczeniowo?
13 gru 20:40
Jerzy:
Adamm ... nie mąć , bo to maksimum
13 gru 20:41
madzia: @Jerzy nie wiem
13 gru 20:41
Jerzy:
Zanak pocchodnej zależy tylko od znaku funkcji: f(x) = −x + 1 ,
a jak ona zmienia znak w punkcie: x = 1 ?
13 gru 20:42
Jerzy:
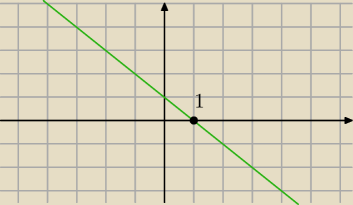
Popatrz...
13 gru 20:43
Janek191:
Dla x < 1 jest f '(x) > 0 , a dla x > 1 jest f '(x) < 0.
13 gru 20:43
madzia: Panowie, powoli
skąd tutaj nagle wzięło się −x+1?
13 gru 20:44
Janek191:
2 − 2 x = 2*( 1 − x) = 2*( − x + 1)
13 gru 20:45
Jerzy:
W pochodnej mianownik jest stale dodatni, a znak licznika zależy tylko od znaku
wyrażenia: 2(1 − x), a on zależy od znaku ( 1 − x), czyli funkcji: y = −x + 1
13 gru 20:45
madzia: Dobrze, zaczynam rozumieć, czyli zmienia znak z dodatniego na ujemny.
13 gru 20:47
madzia: @Jerzy a co teraz?
13 gru 20:48
Jerzy:
A to oznacza ,że funkcja najpierw rośnie, potem maleje, czyli ma .... maksimum.
13 gru 20:48
madzia: no tak maksimum w punkcie x = 1
13 gru 20:49
Jerzy:
Teraz punkty przegięcia i wypukłość/wklęsłość funkcji.
13 gru 20:51
madzia: Czy muszę policzyć pochodną pochodnej?
13 gru 20:58
Jerzy:
Tak ..bez tego ani rusz.
13 gru 20:59
madzia: Na moje to będzie tak:
f''(x) = (−2e)−x − (2−2x)/ex
13 gru 21:05
madzia: Wróc, zapomniałam o mianowniku
13 gru 21:08
madzia: f''(x) = [(−2e)−x − (2−2x)/ex] / e
−2x
@Jerzy co dalej?
13 gru 21:09
Adamm: kiedy funkcja jest wklęsła, wypukła, punkty przegięcia
13 gru 21:09
Adamm: wypukła gdy f''(x)>0, wklęsła gdy f''(x)<0, punkty przegięcia gdy zmienia się znak
13 gru 21:10
madzia: ummm, no tak, wychodzi mi coś takiego :
−2−x > 2e−2x oraz −2−x < 2e−2x i nawet nie wiem jak to dalej ruszyć
13 gru 21:12
Jerzy:
| | −2ex − (2 − 2x)ex | | −4ex + 2xex | | 2(x−2) | |
f"(x) = |
| = |
| = |
| |
| | e2x | | e2x | | ex | |
13 gru 21:13
Jerzy:
Teraz ustalaj jej znak.
13 gru 21:14
Adamm:
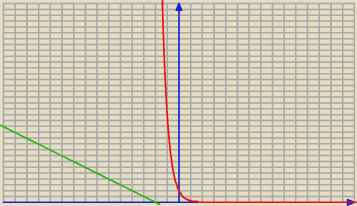
−2−x<2e
−2x dla każdego x
13 gru 21:14
Adamm: to teraz ma więcej sensu
13 gru 21:15
madzia: Dobra Panowie, zaczynam się bardzo gubić w tym momencie, mało co rozumiem..
W tym samym momencie gubię się u Krystiana.. Po prostu wybiorę się jutro na konsultację.
Dzięki za pomoc. Pozdrawiam
13 gru 21:19
Jerzy:
Druga pochodna zeruje się w punkcie x = 2 i zmienia znak,
a więcposiada punkt przegięcia. Dla x <2 funkcja jest wklęsła i odwrotnie.
13 gru 21:21