wyznacz wzór funkcji Elena : wyznacz wzór funkcji kwadratowej która jest: a) malejąca w przedziale (−∞, 1> i rosnąca w przedziale <1,∞) osiąga wartość najmniejszą równą −3 i jej wykres przechodzi przez punkt P=(2,−1) b) malejąca w przedziale (−∞,−3> i rosnąca w przedziale <−3,∞) jednym z jej miejsc zerowych jest x = −5 i jej wykres ma z prostą y= −8 dokładnie jeden punkt wspólny c) rosnąca w przedziale (−∞,3> i malejąca w przedziale <3,∞) ma dokładnie jedno miejsce zerowe i jej wykres przecina oś Oy w punkcie rzędnej −9 Dziękuje i pozdrawiam

===: wydaje mi się, że Elena jest sobowtórem Nikity1234

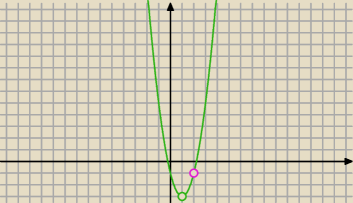
===: a) wiemy zatem, że x_w=1 a>0 f(1)=−3=f_min zatem y=a(x−1)²−3 a skoro P=(2,−1) należy do wykresu to −1=a(2−1)²−3 ⇒ a=2 więc ostatecznie y=2(x−1)²−3

Elena : Zgadza się dzięki za pomoc

Elena : mógłbyś rozwiązać jeszcze podpunkt b i c bylabym wdzięczna