pochodna edd: Wykaz, ze dla x∊ (1;+∞) spełniona jest nierównosc x³−2x²>6−7x

lulu: rozważ y=x³−2x²−6+7x Zauważ, że x=1 jest pierwiastekiem, wiec y=(x−1)(funkcja kwadratowa) Potem łatwo pokazać, że więcej miejsc zerowych nie ma x>1 to y>0 koniec

edd: dzieki a jeszcze jak wykazac ze f(x)=x⁵+5x−1 ma dokladnie jedno miejsce zerowe

edd: f(x)=x⁵+5x−1 f'(x)=5x⁴+5 f'(x)>0 dla x ∊ R zatem f(x) jest rosnąca w R − tylko jedno miejsce zerowe bo jesli było by wiecej musialaby zmalec ok?

Mila: Jeszcze można : f(0)=−1 , f( 1)=5 x₀∊(0,5) z własności Darboux

edd: mam jeszcze b) tez wykazac ze funkcja ma tylko jedno miejsce zerowe

	x
f(x)=
	1−x

	−x
f'(x)=		zatem f'(x) < 0 Dla x ∊ R \ {1}
	(1−x)2

f(x) malejaca dla x ∊ R \ {1} z tego wynika ze ma jedno m. zer wystarczy to?

miś:

	x
f(x)=		Df=R\{1}
	1−x

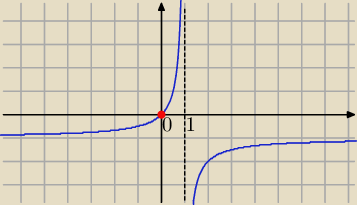
	x
f(x)=0 ⇔		=0 ⇔ x=0 ∊D
	1−x

x=0 −− jest jedynym miejscem zerowym funkcji f(x) i to wszystko

miś: