funkcja kwadratowa yano: Wyznacz te wartości parametru m dla których jedno z rozwiązań równania mx2−(2m+1)x+m−2=0 jest ujemne a drugie większe od 5. W rozwiązaniu pigor napisał: m*f(5)< 0 i m*f(0)<0 ⇔ m(25m−5(2m+1)+m−2)< 0 i m(m−2)< 0 ⇔

	7
⇔ m(16m−7)< 0 /:16 i 0< m < 2 ⇔ m(m−		)< 0 i 0< m < 2 ⇔
	16

	7		7		7
⇔ 0< m<		i 0< m < 2 ⇔ 0< m<		⇔ m∊(0;		)
	16		16		16

Wynik pigora jest właściwy Napewno się mylę ale według mnie powinno być m*f(5)>0 i m*f(0)>0 bo gdy m>0 to f(0)>0 i f(5)>0 gdy m<0 to f(0)<0 i f(5)<0 Proszę o wyjaśnienie

thx: nie sądzę aby pigor napisał m*f(5) bo to głupawka

yano: thx mylisz się narysuj wykres gdy m>0 wtedy f(0)>0 i f(5)>0 narysuj wykres gdy m<0 wtedy f(0)<0 i f(5)<0 to ma sens

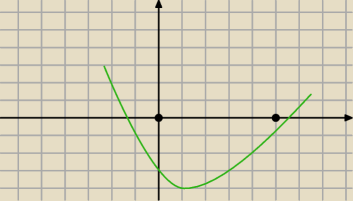
Jerzy: @ jano ... akurat Ty nie masz racji ... popatrz na rysunek.

===: ...i tak to jest kiedy nie podajesz całej treści rozwiązania zadania tylko zaczynasz gdzieś od środka.

yano: pigor spójrz i doradź proszę

Jerzy: Widzę,że nawet rysunek cię nie przekonuje .

yano: przepraszam za zamieszanie dziękuję za pomoc

yano: Jerzy przepraszam przekonuje mnie rysunek

===: yano ... nie zrozumiałeś tego co napisał pigor Idąc Twoją ścieżką nie możesz pisać m*f(5) tylko f(5) pigor zastosował sprytny wybieg bo oba przypadki czyli m>0 i m<0 zawarł w m*f(x) zauważ, że dla dowolnego m ... wykresem m*f(x) jest parabola "uśmiechnięta" i dlatego rozpatruje on tylko m*f(0)<0 i m*f(5)<0 To uwzględnia Twoje oba przypadki