krawędzie akwarium w kształcie prostopadłościanu
CHI: Krawędzie akwarium w kształcie prostopadłościanu, wychodzące z jednego wierzchołka mają
długości 3m, 5m i 2m. Inne akwarium prostopadłościenne, którego każda krawędź jest większa o
ten sam odcinek od odpowiednich krawędzi pierwszego akwarium, ma pojemność o 110 m
3 większą.
Wyznacz wymiary większego akwarium. Bardzo proszę o pomoc

12 sty 21:22
BananTm: (3+x)*(5+x)*(2+x)=(3*5*2)+110 rozwiąż to i masz odp..
12 sty 21:36
CHI: ja wiem tylko że właśnie w tym rozwiązaniu się gubię

12 sty 21:42
nick: to rozwiązanie wychodzi takie że nie wiadomo jak je dalej rozwiązać:
x
3+10x
2+31x−110
co dalej



25 sty 21:59
nick: bo tego to ani sie nie da wyłączyć x przed naiwas, ani rozłożyć wielomianu na czynniki...
25 sty 22:02
ptaszek: 2*3*5=30
30+110 = 140
(2+x)*(3+x)*(5+x)=140
3x2 + 20x + 31 = 140
3x2 +20x −109 = 0
i tu niewiem co dalej probowałem deltą ale pierwiastek z 1708 to jest 41 z kawałkiem
23 mar 13:40
może pomoże:
na innej stronie jest
1 prostopadłościan
3 * 5 * 2=30m(sześciennych)
2 prostopadłoscian DF = x nalezy do R\{−3;−5;−2}
(3+x)(5+x)(2+x)=140
(15 + 3x + 5x + x2)(2+x) = 140
(15 + 8x + x2)(2+x) = 140
30 + 16x + 2x2 + 15x + 8x2 + x3 = 140
x3 + 10x2 + 31x − 110 = 0
wyliczamy pierwiastki wielomianu i podstawiamy za boki np. (3+x) mamy bok czyli za x
podstawiamy pierwiastek i mamy boki.
23 mar 13:42
ptaszek:
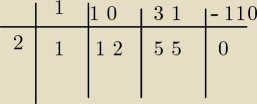
dzięki pomogło

pomyliłem sie w rachunkach
x
3 +10x
2 +31x −110 = 0
dalej schematem hornera
podanym wyzej
z czego wychodzi
(x−2)(x
2 +12x +55) = 0
czyli
x−2=0 ∨ x
2 +12x +55=0
x=2 ∨ Δ=144−220=−76 →brak pierwiastka
x=2
boki: 4,5,7
23 mar 13:57





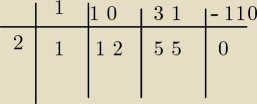 dzięki pomogło
dzięki pomogło  pomyliłem sie w rachunkach
x3 +10x2 +31x −110 = 0
dalej schematem hornera
podanym wyzej
z czego wychodzi
(x−2)(x2 +12x +55) = 0
czyli
x−2=0 ∨ x2 +12x +55=0
x=2 ∨ Δ=144−220=−76 →brak pierwiastka
x=2
boki: 4,5,7
pomyliłem sie w rachunkach
x3 +10x2 +31x −110 = 0
dalej schematem hornera
podanym wyzej
z czego wychodzi
(x−2)(x2 +12x +55) = 0
czyli
x−2=0 ∨ x2 +12x +55=0
x=2 ∨ Δ=144−220=−76 →brak pierwiastka
x=2
boki: 4,5,7