 Należy obliczyć pole trapezu prostokątnego, w który możne być wpisany okrąg, mając dane
długości jego podstaw: a i b.
Należy obliczyć pole trapezu prostokątnego, w który możne być wpisany okrąg, mając dane
długości jego podstaw: a i b.
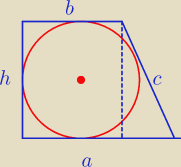 h =2 r
Mamy
a + b = h + c ⇒ a2 + 2 a*b + b2 = h2 + 2 h*c + c2
c2 = h2 + (a − b)2 ⇒ c2 = h2 + a2 −2 a*b + b2
więc
a2 +2 a*b + b2 = h2 +2 h*c + h2 + a2 −2 a*b + b2
4 a*b = 2 h2 + 2 h*c
2 a*b = h2 + h*c = h*( h + c) = h*(a + b)
h =2 r
Mamy
a + b = h + c ⇒ a2 + 2 a*b + b2 = h2 + 2 h*c + c2
c2 = h2 + (a − b)2 ⇒ c2 = h2 + a2 −2 a*b + b2
więc
a2 +2 a*b + b2 = h2 +2 h*c + h2 + a2 −2 a*b + b2
4 a*b = 2 h2 + 2 h*c
2 a*b = h2 + h*c = h*( h + c) = h*(a + b)
| 2 a*b | ||
h = | ||
| a + b |
| 2 a*b | ||
P = 0,5 ( a + b)*h = 0,5 *( a + b)* | = a*b | |
| a + b |
 Mam tylko pytanie (ponieważ wcześniej się z tym nie spotkałam), czy zawsze w przypadku trapezów
prostokątnych można stosować założenie a+b=h+c ?
Mam tylko pytanie (ponieważ wcześniej się z tym nie spotkałam), czy zawsze w przypadku trapezów
prostokątnych można stosować założenie a+b=h+c ?
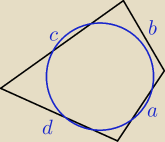 nie zawsze
takie założenie stosujemy jedynie wtedy gdy w trapez można wpisać okrąg
ogólnie, jeśli w czworokąt (dowolny) da się wpisać okrąg, to a+c = b+d (wg oznaczeń na moim
rysunku)
nie zawsze
takie założenie stosujemy jedynie wtedy gdy w trapez można wpisać okrąg
ogólnie, jeśli w czworokąt (dowolny) da się wpisać okrąg, to a+c = b+d (wg oznaczeń na moim
rysunku)

