Zadanie nr 10 fg Wałowa: Uzasadnij ze odleglosc dowolnych dwoch punktow kola nie przekracza liczby 2r

xxx: co tu uzasadniać?

Kacper: Warto poczytać definicję koła.

Wałowa: nagorszse sa walsnie takie proste rzeczy do udowodnienia Oczywiscie ze tak bedzie . Kacper znam definicje kola Kolem o srodku O i prpmieniu r nazywamy zbior punktow plaszczyzny ktorych odleglosc od punktu O jest mniejsza lub rowna r W zwiazku z tym powstaje nastepny problem czy odleglosc np 4 , 5 i n punktow tez nie nie przekracza 2r?

Wałowa: xxx potrafisz to uzasadnic ?

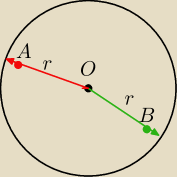
Wałowa: O A≤r OB≤r ============= OA+OB≤2r Teraz dla kilku punktow jak bedzie ?

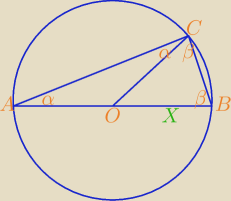
Rafal: Domyślam się, że chodzi o maksymalnie uproszczone rozwiązanie. Rozpatrzmy okrąg o środku w punkcie O i promieniu długości r. Niech A, B i C będą takimi punktami leżącymi na tym okręgu, że |AB|=2r (takie punkty A i B istnieją − leżą na przecięciach pewnej prostej przechodzącej przez punkt O z danym okręgiem) oraz C≠B. Niech kąty BAC i ABC mają miary kolejno α i β. Z równości |AO|=|CO| i |BO|=|CO| wynika, że kąty ACO i BCO także mają miary α i β. W trójkącie ABC: 2α+2β=180⇔α+β=90, zatem kąt ACB to kąt prosty. Niech X będzie takim punktem na prostej AB, że |AX|=|AC|, przy czym punkt X leży po tej samej stronie punktu A co punkt B.

	180−α		1
W trójkącie równoramiennym AXC kąt ACX ma miarę		=90−		α.
	2		2

	1
Z nierówności 90−		α<90 wynika, że punkt X znajduje się pomiędzy punktami A i B, więc
	2

|AX|<|AB|=2r. Równość zachodzi, gdy punkty B i C pokrywają się.

Rafal: Aha, jeśli mamy dwa punkty leżące wewnątrz okręgu, to prowadzimy analogiczne rozumowanie dla cięciwy przechodzącej przez te punkty (oczywiście ta cięciwa jest dłuższa od odcinka utworzonego przez te dwa punkty).

Kacper: Jak chcesz zdefiniować odległość dla 3 punktów w kole?

Wałowa: Rafal dziekuje Ci bardzo Nie wiem czy problem z wieksza iloscia punktow niz 2 to 1 klasa liceum bo to zadnie z 1kalsy liceum z dwoma punktami Problem z wieksza iloscia postawilem sam

Wałowa: Kacper to wynika z tego ze taki problem mozemy postawic tylko dla okregu ?

Kacper: Na okręgu oczywiście nie ma co pokazywać. Odległość każdych dwóch punktów na okręgu jest mniejsza lub równa 2r. Natomiast w kole dla dwóch jest to samo, a dla trzech i więcej trzeba dopowiedzieć co rozumiemy pod pojęciem odległości.

Wałowa: Wiec w okregu dla 3 punktow np A B C AC<AB+BC

Wałowa: Juz dopowiadam Na plaszczyznie okreslona jest odleglosc tj kazdym dwom punktom A b przyporazdkowana jest liczba AB ≥0 przy czym odleglosc spelnia nastepujace warunki AB=0 ⇔gdy A=B AB=BA AB+BC≥AC dla dowolnych punktow A B C

Kacper: Nie ma nic o odległości między 3 punktami

Wałowa: Dobrze . Rozumiem . Dziekuje