trójkąt Hubert: W trójkacie ABC dane są |AB|=14 , |AC|=9, |∡BAC|=60^o Na boku AC obrano punkt M tak,że |MC|=8 i przez punkty M i C poprowadzono okrąg który jest styczny do boku AB w punkcie N Oblicz długość promienia tego okręgu Rysunek zrobiłem no i nie mam pomysłu Pomożecie mi

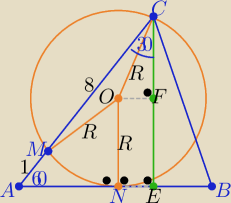Eta: 1/ Z twierdzenia o stycznej i siecznej : |AN|²=|AC|*|AM| ⇒ |AN|²=9*1 ⇒ |AN|=3 2/ Z trójkąta CAE o kątach 30^o, 60^o, 90^o

	9		9
|AE|=		i |CE|=		√3
	2		2

3/ Czworokąt ONEF jest prostokątem o bokach długości

	9		3
R=|EF| i |NE|=|AE|−|AN|=		−3=
	2		2

4/ Z twierdzenia Pitagorasa w ΔCOF:

	3		9		9√3−2R
wiedząc ,że |OF|=|NE|=		i |CF|=|CE|−|FE| =		√3−R =
	2		2		2

mamy:

	3		(9√3−2R)2
R2=(		)2+		/*4
	2		4

	7√3
4R2= 9+81*3−36√3R+4R2 ⇒ ............ R=
	3