ttt wiktoria: wykaz ze funkcja f(x)= |x−1| nie jest rozniczkowalna w punkcie x₀ = 1 dla x≥1 dla x<1 f(x)= x−1 f(x)= −x+1 zatem

	x−1−0		x−1
iloraz różniczkowy		=		= 1
	x−1		x−1

	−x+1−0		−(x−1)
lub		=		= −1
	x−1		x−1

Dobrze to jest? a jesli nie to jak to wykazac Mila juz mi podobny rozwiazywała ale tam liczyła granice ilorazu rozniczkowego a tutaj w ogole dwa rozne chyba wychodza ?

Mila: f(x)=x−1 dla x−1≥0⇔dla x≥1 f(x)=−x+1 dla x<1 Wzór:

	f(x)−f(x0)
limx→x0
	x−x0

⇔

	x−1−(1−1)		x−1
limx→1+		=limx→1+		=1
	x−1		x−1

	−x+1−(−1+1)		−x+1		−(x−1)
limx→1−		=limx→1−		=limx→1−		=−1
	x−1		x−1		x−1

f(x) nie jest różniczkowalna w x=1 ponieważ granica prawostronna ilorazu różnicowego jest różna od lewostronnej. Granica ilorazu różnicowego

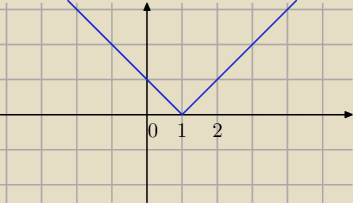Mila: W x=1 na wykresie masz "szpic" , tu nie ma pochodnej. Funkcja jest ciągła w x=1 ale nie jest różniczkowalna w x=1.