Granica i pochodna funkcji
krokus: | | x | | x | |
Funkcja f(x)= |
| − sin x jest ciągła. Wykaż, że równanie |
| − sin x =0 ma co najmniej |
| | 2 | | 2 | |
trzy pierwiastki w przedziale <−π;π>.
10 gru 22:17
Adamm: f'(x)>0 ⇔ x∊(π/3+2kπ;5π/3+2kπ)
mamy ekstrema w punktach x=−π/3, x=π/3
| | π | | π | |
f(−π)=− |
| , f(−π/3)=− |
| +√3/2>0, mamy rozwiązanie dla x∊(−π;−π/3) |
| | 2 | | 6 | |
| | π | |
f(π/3)= |
| −√3/2<0, mamy jedno rozwiązanie dla jakiegoś x∊(−π/3;π/3) |
| | 6 | |
| | π | |
f(π)= |
| >0, mamy rozwiązanie dla x∊(π/3;π) |
| | 2 | |
10 gru 22:34
Adamm: i nie mamy co najmniej 3 pierwiastki, my wiemy że na tym przedziale są 3 pierwiastki
10 gru 22:36
Eta:
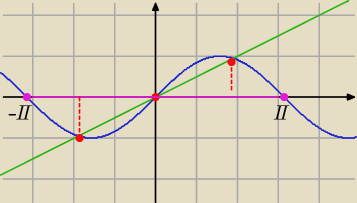
10 gru 22:43
Adamm: graficznie też można było

10 gru 22:44
krokus: Dziękuję

10 gru 22:45


