nierówność jh:

	−2x−1
Jak rozwiązać nierówność		>0 czy mogę to przemnożyć przez kwadrat mianownika?
	−x2−x+2

czy znak > pozostaje bez zmian? Proszę o wytłumaczenie

jh: .

Eta:

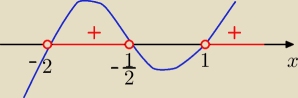
2x+1
	>0 x2+x−2≠0 ⇒(x+2)(x−1)≠0 ⇒ x≠−2, x≠1
x2+x−2

(2x+1)(x+2)(x−1)>0 x∊ .........................

jh:

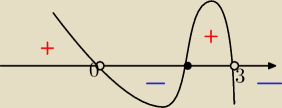
	−4x2+9
a więc czy nierówność		>0 wygląda tak jak na moim rysunku? Dziedzina
	2√3x−x2

funkcji to x∊(0,3)

Adamm: 3x−x²>0 ⇔ x(3−x)>0 ⇔ x∊(0;3) 4x²−9<0

	3		3
−		<x<
	2		2

dobierasz punkty, masz x∊(0;3/2)

jh:

	−4x2+9x
przepraszam, zapomniałem x w liczniku. powinno być
	2√3x−x2

jh: czarna kropka na osi to 9/4

Adamm: 4x²−9x<0 x(x−9/4)<0 x∊(0;9/4)

Jh: A co dzieje się z mianownikiem?

Adamm: mnożymy, jest dodatni

Jh: W przykładzie eta dlaczego przemnozylismy przez kwadrat mianownika? Przepraszam że tak męczę ale mam problem z tymi działaniami

Adamm: bo nie znamy znaku, a nikt nie będzie rozpatrywał przypadków

Jh: I wtedy trzeba zmienić znak > na przeciwny?

Adamm: nie, jak mnożysz razy dodatnią to znak zostawiasz