Jeżeli mam f(x)=U{x^2+1}{x^2-4} oraz jej pochodną f'(x)=U{-8x-2}{(x^2-4)^2} a j
Marzenkaaa: | | x2+1 | | −8x−2 | |
Jeżeli mam f(x)= |
| oraz jej pochodną f'(x)= |
| |
| | x2−4 | | (x2−4)2 | |
a jej maksimum wynośi dla x=−1/4 to jak mam określić przedziały monotoniczności tej funkcji?
Mam odczytać z rysunku f(x)? Czy może f'(x)? Proszę pomocy!

10 gru 15:18
Jerzy:
Monotoniczność funkcji określamy na podstawie znaku pochodnej !
10 gru 15:19
Jerzy:
Tutaj znak pochodnej zależy od znaku licznika,bo mianownik jest stale dodatni
10 gru 15:20
Marzenkaaa:
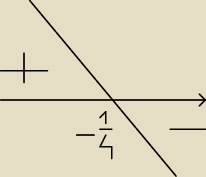
Z lewej strony jest dodatnia a z prawej ujemna. Tylko co dalej
10 gru 15:23
Jerzy:
Tam gdzie pochodna jest dodatnia funkcja rośnie i odwrotnie,
tam gdzie jest ujemna, funkcja maleje.
10 gru 15:26
Marzenkaaa: A jak sprawdzić do którego punktu pochodna maleje/rośnie?
10 gru 15:30
Jerzy:
Dla: −8x − 2 > 0 pochodna jest dodatnia
Dla: −8x − 2 < 0 pochodna jest ujemna
10 gru 15:54
Marzenkaaa: Dziękuję z całego serca Jerzy, naprawdę. Za cierpliwość oraz tłumaczenia. Już powoli to chwytam

Dziękuję ślicznie jeszcze raz
10 gru 16:03
Jerzy:

10 gru 16:05
Jerzy:
Często w tego typu zadaniach mamy sytuację, gdzie znak pochodnej zależy od znaku
jej licznika , bo mianownik jest stale dodatni lub stale ujemny.
10 gru 16:07

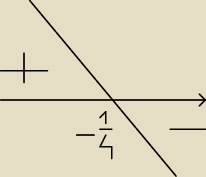 Z lewej strony jest dodatnia a z prawej ujemna. Tylko co dalej
Z lewej strony jest dodatnia a z prawej ujemna. Tylko co dalej
 Dziękuję ślicznie jeszcze raz
Dziękuję ślicznie jeszcze raz
