Nierówność 00000: x²*(5+x)>0, Jak zrobię tak: że skoro x²>0 x>0 i x>−5 to jak to zaznaczę na osi to mam najpierw przedział od 0 do +∞, a potem od −5 do +∞, czyli ogólnie przedział dla tej nierównośi to chyba powinna być część wspólna tych przedziałów, czyli od 0 do +∞, a w odpowiedziach piszą, że (−5,0) Jak to zrobić?

Jerzy: x²*(5+x) > 0 ⇔ x² > 0 i 5 + x > 0 ⇔ x ≠ 0 i x > − 5 ⇔ x ∊ (−5;0) U (0;+∞)

Jerzy: W odpowiedzi masz błąd.

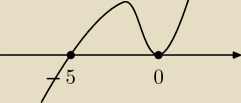
Jack: zle robisz. x²(5+x) > 0 zaznaczamy na osi 0 oraz − 5 A nastepnie rysujemy krzywa. wspolczynnik przy najwyzszej potedze iksa jest dodatni (bo jak bysmy wymnozyli to by bylo 5x² + x³) zatem jest "1" przy x³, a 1 > 0 wiec zaczynamy rysowac od gory (bo dodatni wspolczynnik) od prawej strony Jednakze od zera sie odbija, ta krzywa, bo mamy x² czyli pierwiastek dwukrotny. dla k−krotnych parzystych sie odbija,a dwa jest parzyste wiec odbijamy i przez 5 normalnie przechodzi. zatem rozw. to przedzial x ∊ (−5;0) U (0;∞)

Jerzy: Jack ... po co tyle zachodu ? a* b > 0 ( i a ≥ 0) ⇔ a ≠ 0 i b > 0

00000: o matko, dziękuję

Jack: po to zeby bylo uniwersalnie , bo jak by nie bylo x² tylko x , to skad wiesz jakby kolega zrobil?