Hej, jak policzyć extremum tej funkcji? f(x)=U{x^2}{(x^2-9} pochodna mi wyszła Marzenkaaa: Hej, jak policzyć extremum tej funkcji?

	x2
f(x)=
	(x2−9

pochodna mi wyszła

	−18x
f'(x)=
	(x2−9)2

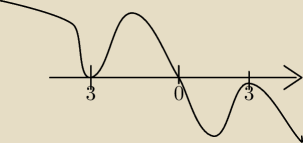
tylko nie wiem co dalej Narysowałam wykres, miejsca 0 to −3 0 oraz 3 , poprowadziłam wykres tylko nie wiem zupełnie co dalej ;c

Jerzy: Ekstremum istnieje tylko w punkcie x = 0 Jak pochodna zmienia znak w punkcie x = 0 ?

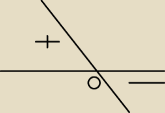
Marzenkaaa: Czyli w 0 funkcja osiąga tylko maksimum, tak?

Jerzy: Tak , bo dla x < 0 funkcja rośnie, a dla x > 0 funkcja maleje.

Marzenkaaa: Dziękuję

Marzenkaaa: A jak określić przedziały monotoniczności tej funkcji?

Jerzy: Tam gdzie pochodna jest dodatnia funkcja rośnie, tam gdzie ujemna, maleje.

Marzenkaaa: Mam rozumieć, że od (−∞;−3)u(−3;0) rośnie, a (0;3)u(3;∞) maleje?

Jerzy: NIe ... intresuje cię tylko znak pierwszej pochodnej.

Jerzy: Zastanów się .. .gdyby było tak jak piszesz, funkcja miałaby więcej eksremów lokalnych.

Marzenkaaa: Ech to niestety nie wiem. Nie umiem powiedzieć gdzie rośnie gdzie maleje

Jerzy: Przypatrz się pochodnej .... od czego zależy jej znak ?

Marzenkaaa: Od tego czy jest w danym punkcie minimum czy maximum?

Jerzy: Pytam o znak pochodnej, kiedy pochodna jest dodatnia , a kiedy ujemna ?

Marzenkaaa: Jeżeli mamy to x0 i w niej jest maskimum, to z lewej strony tego punktu funkcja jest rosnąca czyli dodatnia, a z prawej wtedy malejąca, czyli ujemna

Jerzy: Tak... pochodna jest dodatnia dla: x < 0 i ujemna dla x > 0. Funkcja jedno ekstremum lokalne w punkcie : x = 0 ( maksimum )

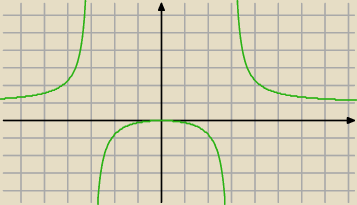
Jerzy: Tutaj masz wykres tej funkcji.