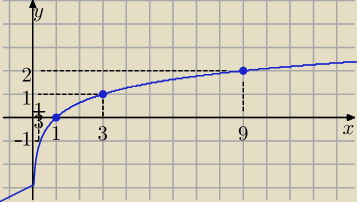
POMOCY, POTRZEBNE NA JUŻ Kasiiikaa: 1. Oblicz a) 6¹⁻ √2 * 6 √2+1 = 2. rozwiąż równania a) log(na dole2)x +log(na dole 2 ) (x−3)=2 b) 4^x+1=256 3.Sporządź wykres funkcji f(x)=log (na dole 3 ) x

Jerzy: Tutaj nie ma jasnowidzów.

Eta: 1/

	1
a) 61−√2*61+√2= 61−2=
	6

2/ a) x>3 log₂x(x−3)=2 x(x−3)= 4 i x>3 ⇒ x=4 b) 4*4^x=256 4^x= 64 ⇒ x=3

Eta: Chyba,że .......... są

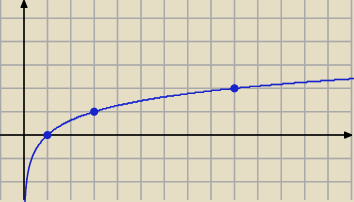
Eta: 3 wykres .... bez tej kreseczki po lewej

Jerzy: Widzę ,że jednak są jasnowidze

Janek191: Eta, to jasnowidz pierwszego sortu

xxxx: (sinx+cosx)²=( \frac{3 \sqrt{5} }{5})²= \frac{9}{5}sin²x+2sinxcosx+cos²x= \frac{9}{5} 1+2sinxcosx= \frac{9}{5}2sinxcosx= \frac{4}{5}sinxcosx= \frac{2}{5}sinx= \frac{2}{5cosx} sin²x+cos²x=1\frac{4}{25cos²x}+cos²x=1 \frac{4}{25}+cos⁴x=cos²xcos²x=tt²−t+ \frac{4}{25}=0 \Delta =1− \frac{16}{25}= \frac{9}{25} \sqrt{ \Delta } = \frac{3}{5}t₁= \frac{1− \frac{3}{5} }{2}= \frac{1}{5} t₂= \frac{1+ \frac{3}{5} }{2}= \frac{4}{5}*) cosx= \frac{ \sqrt{5} }{5}**) cosx= \frac{2 \sqrt{5} }{5} *) sinx= \frac{2}{5} \cdot \frac{5}{ \sqrt{5} }= \frac{2 \sqrt{5} }{5}**) sinx= \frac{2}{5} \cdot \frac{5}{2 \sqrt{5} }= \frac{ \sqrt{5} }{5}

edyta: L =315