| 1 | ||
lim n→∞ | ile wynosi ta granica i dlaczego ? | |
| sin2n |
 Faktycznie, parę linii niżej są szeregi.
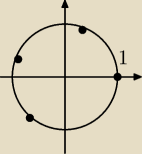
Rysunek. Każdy następny punkt leży w odległości 1 (mierzonej po okręgu) po lewej
od ostatniego. π jest niewymierne, więc żadne punkty na znajdą się w tym samym miejscu.
Jak postawimy n punktów, to jakieś dwa znajdą się w odległości mniejszej niż 2π/n.
Jeśli to były punkty k i j, k<j, to tak samo będzie z punktami 0 i j−k=m.
Punkt m leży w odległości mniejszej od 2π/n od 0.
|sin m | < |sin 2π/n| < 2π/n
Wniosek. Znajdziemy podciąg rozbieżny do ∞. Więcej, dla każdej liczby x ≥ 1,
znajdziemy podciąg zbieżny do x. Ale to pozostawiam do samodzielnego uzupełnienia.
Proszę poprawić ewentualne usterki.
Faktycznie, parę linii niżej są szeregi.
Rysunek. Każdy następny punkt leży w odległości 1 (mierzonej po okręgu) po lewej
od ostatniego. π jest niewymierne, więc żadne punkty na znajdą się w tym samym miejscu.
Jak postawimy n punktów, to jakieś dwa znajdą się w odległości mniejszej niż 2π/n.
Jeśli to były punkty k i j, k<j, to tak samo będzie z punktami 0 i j−k=m.
Punkt m leży w odległości mniejszej od 2π/n od 0.
|sin m | < |sin 2π/n| < 2π/n
Wniosek. Znajdziemy podciąg rozbieżny do ∞. Więcej, dla każdej liczby x ≥ 1,
znajdziemy podciąg zbieżny do x. Ale to pozostawiam do samodzielnego uzupełnienia.
Proszę poprawić ewentualne usterki.