macierz 5x5
marek: obliczyć wyznacznik macierzy 5x5
1 0 0 3 −1
3 −2 0 0 2
1 1 0 0 1
2 0 4 1 −2
−1 1 7 0 3
9 gru 13:42
Omikron: Wybierz trzecią kolumnę, najwięcej zer jest. Potem będziesz musiał jeszcze obliczyć wyznaczniki
dwóch macierzy 4x4
9 gru 14:38
Jack:
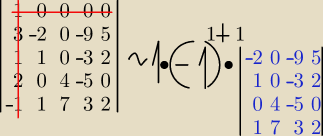
najszybciej bedzie "wyzerowac" pierwszy wiersz.
zrobimy to np. tak
k
4' = k
4 + (−3)k
1
k
5' = k
5 + k
1
wynikiem tego bedzie (patrz rysunek)
(czerwonym jest wykreslenie) − z Laplace'a i niebieskim to co otrzymamy
9 gru 14:46
marek: później i tak nie potrafię tego ruszyć dalej chciałam wyzerować kolumne piątą ale te −2 w
pierwszej kolumnie mi przeszkadza
9 gru 15:11
Omikron: Podstaw do wzoru, zero filozofii
9 gru 15:22
marek: nie piątą tylko czwartą Jack dalej chciałam wyzerować
9 gru 15:26
Jack:
marek − "chciał
am" ?

Niestety nic nie widze poki co innego, wiec wejdziemy w ulamki...
w kolumnie drugiej mamy 2 zera oraz w wierszu 3.
"Wyzerujmy" kolumne druga pozbywajac sie czworki.
wtedy otrzymujemy w wierszu trzecim :
pozostale wiersze bez zmian.
zatem wykreslamy z rozw. Laplace'a kolumne druga, wiersz czwarty i mamy :
... = 7*(−1)
6 *
|−2 −9 5|
|−1 −3 2|
9 gru 15:54
marek: a wiesz może czy mogę to jak Ty tam skończyłeś przemnożyć przez tą jedynkę i dalej kontynuować
twierdzeniem Laplace'a

?
9 gru 16:13
Jack: no to wlasnie zrobilem?
Hmm, nie rozumiem co masz na mysli
9 gru 16:27
marek: ja kontynuując tą macierz 4x4 rozwinięciem laplacea względem trzeciego wiersza bo tam są dwa
zera otrzymałem wynik −531 dobrze?
9 gru 16:31
Benny: https://www.wolframalpha.com/input/?i=matrix+%7B%7B1,0,0,3,-1%7D,%7B3,-2,0,0,2%7D,%7B1,1,0,0,1%7D,%7B2,0,4,1,-1%7D,%7B-1,1,7,0,3%7D%7D
9 gru 16:36
Benny: Poprawka
https://www.wolframalpha.com/input/?i=matrix+%7B%7B1,0,0,3,-1%7D,%7B3,-2,0,0,2%7D,%7B1,1,0,0,1%7D,%7B2,0,4,1,-2%7D,%7B-1,1,7,0,3%7D%7D
Twój wynik jest dobry.
9 gru 16:42
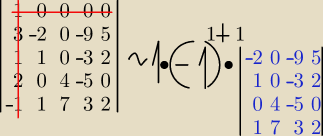 najszybciej bedzie "wyzerowac" pierwszy wiersz.
zrobimy to np. tak
k4' = k4 + (−3)k1
k5' = k5 + k1
wynikiem tego bedzie (patrz rysunek)
(czerwonym jest wykreslenie) − z Laplace'a i niebieskim to co otrzymamy
najszybciej bedzie "wyzerowac" pierwszy wiersz.
zrobimy to np. tak
k4' = k4 + (−3)k1
k5' = k5 + k1
wynikiem tego bedzie (patrz rysunek)
(czerwonym jest wykreslenie) − z Laplace'a i niebieskim to co otrzymamy
 Niestety nic nie widze poki co innego, wiec wejdziemy w ulamki...
w kolumnie drugiej mamy 2 zera oraz w wierszu 3.
"Wyzerujmy" kolumne druga pozbywajac sie czworki.
Niestety nic nie widze poki co innego, wiec wejdziemy w ulamki...
w kolumnie drugiej mamy 2 zera oraz w wierszu 3.
"Wyzerujmy" kolumne druga pozbywajac sie czworki.
 ?
?