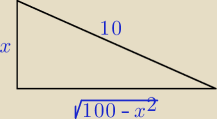
Optymalizacja Alky: Rozważamy trójkąty prostokątne których przeciwprostokątne mają długość 10 . Znajdź długości przyprostokątknych trójkąta, który ma największe pole. Oblicz to pole . Mam mały problem z pochodną i wyznaczeniem z niej później ekstremum . Ktoś coś ?

yht: a²+b² = 10² b = √100−a²

	a*b		a*√100−a2		√a2*√100−a2		√a2(100−a2)
P =		=		=		=		=
	2		2		2		2

	√100a2−a4
=
	2

by podstawił t=a² to może nawet bez pochodnej by się udało

marta: Największe pole ma trójkąt prostokątny równoramienny o ramieniu : a=5√2

	a2		c2
P=		= 25 [j2] lub P=		= 25
	2		4

Bogdan:

	1
Pole P =		x√100 − x2
	2

	1
Wyznaczamy maksimum funkcji P(x) =		√100x2 − x4
	2

Założenie: −x²(x − 10)(x + 10) ≥ 0 i x > 0

	200x − 4x3		−4x(x2 − 50)
P'(x) =		=		= ...
	2√100x2 − x4		2x√100 − x2

stąd funkcja P(x) osiąga maksimum dla x = 5√2

Alky: No tyle, że ma być 45 45 90 o takim boku to wiem ale to trzeba udowodnić obliczeniami [P[yht] jak byś to robił bez z pochodną, bo własnie w tym momencie się zacinam bo pochodna wychodzi niefajna

Alky: Ok zaraz ogarne

marta:

	a2b2
P2=		a2= 100−b2 , 0< a,b<c
	4

	b4
P2(b)= −		+50b2
	4

[P²(b)]^'= −b³+50b ........................ a=5√2 i b= 5√2 P= 25

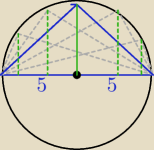
yht: gdzieś widziałem rozwiązanie tego zadania z wykorzystaniem własności trójkąta opartego na średnicy okręgu, wyglądało to mniej więcej tak jak na tym rysunku każdy Δ oparty na średnicy jest prostokątny

	a*h
widać że pole P =		, przy nie zmieniającej się podstawie a=10, będzie największe
	2

jeśli h=5 będzie promieniem okręgu stąd wynikają długości przyprostokątnych trójkąta, obie po 5√2

marta: A co zrobisz jak będzie to zadanie z serii ....... zakodowania wyniku ? ( też wykonasz takie obliczenia z pochodną ? a= ..... zakoduj wynik trzech miejsc po przecinku

Alky: Ok, wróciłem po chwili przerwy . Takiego zadania raczej nie byłoby kodowanego, bo w takich przypadkach to prawie zawsze ( zależy od zadania ) sąto prostokąty, sześciany, trójkąt 45 45 90 etc . Dzięki wszystkim za pomoc

Jack: alki, spojrz na twoj poprzedni post z zadaniem