pochodna
Alky: | | 1 | |
Jak policzyć pochodną z tego |
| √100−b2*b |
| | 2 | |
8 gru 19:09
Adamm: | | 1 | | 1 | 1 | | 1 | |
( |
| √100−b2*b)' = |
|
| *(−2b)*b+ |
| √100−b2= |
| | 2 | | 2 | 2√100−b2 | | 2 | |
| | 1 | | b2 | |
= |
| ( |
| +√100−b2) |
| | 2 | | √100−b2 | |
8 gru 19:12
Adamm: użyłem wzoru na pochodną funkcji złożonej, jak chcesz bez tego to licz z definicji
8 gru 19:17
Jack:
jesli potrzebujesz to do policzenia np. maxymalnej objetosci czy czegokolwiek innego
to zawsze mozesz podstawic inna funkcji, przy czym to "b" musisz wciagnac fo pierwiastka.
| | 1 | | 1 | |
tzn. |
| √b2(100−b2) = |
| √−b4 + 100b2 |
| | 2 | | 2 | |
Teraz niech bedzie dana funkcja g = −b
4 + 100b
2
| | 1 | |
osiaga ona ekstremum dla tego samego argumentu co funkcja |
| √−b4 + 100b2 |
| | 2 | |
zatem mozesz policzyc ekstrema dla funkcji g, a wartosci to potem juz do tej normalnej funkcji
8 gru 19:20
Alky: No wiem wiem, widzę, tylko ta pochodna wychodzi taka niesympatyczna. Może inaczej.
Zadanie :
Rozważamy trójkąty prostokątne których przeciwprostokątne mają długość 10 . Znajdź długości
przyprostokątknych trójkąta, który ma największe pole. Oblicz to pole .
Generalnie to takie typowe zadanie optymalizacyjne.
z a2+b2=100 wyznaczyłem sobie a=√100−b2 i do wzoru 1/2ah(w tym przypadku 1/2ab) . Teraz
pochodna z tego tylko wychodzi taka nie fajna własnie . Jakiś inny sposób, albo pokazać mi
gdzie się pomyliłem ? A może ta pochodna ma taka wyjść, choć nie wiem bo to takie zwykłe
prostsze zadanie
8 gru 19:25
Alky: Dobra, jestem imbecylem :X
Dzięki Jack .... Bo to nie jest tak, że b = √b2 .. Shame on me
8 gru 19:26
Jack:
b = √b2 dla b ≥ 0
8 gru 19:28
Alky: Tak, jasne . Gimnazjum. Jest bardzo źle jak nie zauważyłem czegoś takiego ......
8 gru 19:30
Jack:
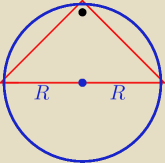
jesli nie optymalizacyjnie to zawsze mozna tak :
Skoro rozpatrujemy trojkaty prostokatne, to znaczy ze mozna na tych trojkatach opisac okregi,
co wiecej srednice okregow to przeciwprostokatne trojkata.
| | 1 | |
Pole trojkata : P = |
| a * h |
| | 2 | |
skoro a = 2R (bo srednica okregu)
to maksymalne pole uzyskamy dla najwiekszego "h" a to h z kolei jest najwieksze, gdy jest
promieniem tego okregu.
stad skoro przeciwprostokatna = 2R = 10 to R = 5
| | 1 | | 1 | |
zatem pole maxymalne : P = |
| a*h = |
| * 2R * R = R2 = 25 |
| | 2 | | 2 | |
8 gru 19:41
Alky: No niestety jest optymalizacyjnei muszęstandardowo do tego dojść

Sprawa
√25b−1/4 b4
8 gru 20:01
Alky: b4 jest w liczniku. Jaka będzie z tego pochodna ?
8 gru 20:01
Alky: | | 1 | |
Wyszła mi |
| ale nie jestem pewny |
| | 2√50b−b3 | |
8 gru 20:02
Jack:
nie czaje zapisu...
| | b4 | |
25b − |
| i to wszystko pod pierwiastkiem? |
| | 4 | |
no to to jest pochodna zlozona...
| | b4 | | 1 | | b4 | |
(√25b − |
| )' = |
| * (25b − |
| )' = |
| | 4 | | | | 4 | |
8 gru 20:12
Alky: Generalnei to jestem w klasie maturalnie więc pochodna złożona jest jeszcze nielegalna

Możesz rozpisać jak być robił to zadanie które napisałem w poście 19:25 , bo raczej nie sądzę
żeby tu była konieczność liczenia pochdnej złożonej . Sorki za zawracanie głowy

8 gru 20:18
Jack:
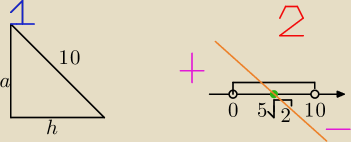
ja w maturalnej mialem pochodne zlozone.
Ale mowie, ze nie musisz... dobra, zadanie :
Rozważamy trójkąty prostokątne których przeciwprostokątne mają długość 10.
Znajdź długości przyprostokątnych trójkąta, który ma największe pole. Oblicz to pole .
Zatem
| | 1 | |
Pole trojkata = |
| * a * h |
| | 2 | |
z Pitagorasa (patrz rysunek oznaczony
1)
a
2 + h
2 = 100
a =
√100−h2 [założenie h ∊ (0;10)]
zatem
| | 1 | | 1 | | 1 | |
P(a) = |
| h√100−h2 = |
| √h2(100−h2) = |
| √−h4+100h2 |
| | 2 | | 2 | | 2 | |
Niech f(h) = −h
4 + 100h
2
Osiaga ona ekstrema dla tych samych argumentow co funkcja P(a).
f ' (h) = − 4h
3 + 200h
f ' (h) = 0
− 4h
3 + 200h = 0
h(−4h
2+200) = 0
h = 0 (sprzeczne) lub 4h
2 = 200
h
2 = 50
h =
√50=
√25*2 = 5
√2
Zaznaczamy na osi (patrz rysunek oznaczony
2)
zaznaczamy przedzial do ktorego nalezy h, tzn (0;10)
nasza pochodna byla (f ' (h) = − 4h
3 + 200h) zatem przy najwiekszej potedze wspolczynnik
ujemny, rysujemy od prawej strony od dolu − patrz brazowy kolor.
No i piszemy podsumowanie
dla h ∊ (0; 5
√2> f'(h) > 0 zatem funkcja rosnie
dla h ∊ <5
√2;10) f'(h) < 0 zatem funkcja maleje
dla h = 5
√2 funkcja osiaga ekstremum i jest to maksimum.
Zatem
h = 5
√2
a
2 = 100 − h
2 = 100 − 50 = 50
a =
√50 = 5
√2
zatem a = h = 5
√2
P
max = (i teraz wstawiamy do tego wzoru z pierwiastkiem)
| | 1 | | 5√2 | | 25*2 | |
= |
| *5√2*√100−(5√2)2 = |
| * 5√2 = |
| = 25 |
| | 2 | | 2 | | 2 | |
8 gru 21:07
Jack: ?

8 gru 21:53
Alky: O kurde , ładnie

Napracowałeś się

Myślałem że już poszedłeś al mi zależało na tym
zadaniu.
*
Niech f(h) = −h4 + 100h2
Osiaga ona ekstrema dla tych samych argumentow co funkcja P(a).
*
To jest moment którego mi było trzeba . Własnie miałem problem z tą pochodną jak bym chciał to
liczyć pod schemat, bo generalnei zadanie było takie typowe.
Na prawdę dzięki wielkie za poświęcony czas

8 gru 22:14
 jesli nie optymalizacyjnie to zawsze mozna tak :
Skoro rozpatrujemy trojkaty prostokatne, to znaczy ze mozna na tych trojkatach opisac okregi,
co wiecej srednice okregow to przeciwprostokatne trojkata.
jesli nie optymalizacyjnie to zawsze mozna tak :
Skoro rozpatrujemy trojkaty prostokatne, to znaczy ze mozna na tych trojkatach opisac okregi,
co wiecej srednice okregow to przeciwprostokatne trojkata.
 Sprawa √25b−1/4 b4
Sprawa √25b−1/4 b4
 Możesz rozpisać jak być robił to zadanie które napisałem w poście 19:25 , bo raczej nie sądzę
żeby tu była konieczność liczenia pochdnej złożonej . Sorki za zawracanie głowy
Możesz rozpisać jak być robił to zadanie które napisałem w poście 19:25 , bo raczej nie sądzę
żeby tu była konieczność liczenia pochdnej złożonej . Sorki za zawracanie głowy 
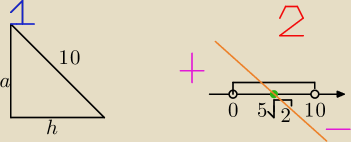 ja w maturalnej mialem pochodne zlozone.
Ale mowie, ze nie musisz... dobra, zadanie :
Rozważamy trójkąty prostokątne których przeciwprostokątne mają długość 10.
Znajdź długości przyprostokątnych trójkąta, który ma największe pole. Oblicz to pole .
Zatem
ja w maturalnej mialem pochodne zlozone.
Ale mowie, ze nie musisz... dobra, zadanie :
Rozważamy trójkąty prostokątne których przeciwprostokątne mają długość 10.
Znajdź długości przyprostokątnych trójkąta, który ma największe pole. Oblicz to pole .
Zatem

 Napracowałeś się
Napracowałeś się  Myślałem że już poszedłeś al mi zależało na tym
zadaniu.
*
Niech f(h) = −h4 + 100h2
Osiaga ona ekstrema dla tych samych argumentow co funkcja P(a).
*
To jest moment którego mi było trzeba . Własnie miałem problem z tą pochodną jak bym chciał to
liczyć pod schemat, bo generalnei zadanie było takie typowe.
Na prawdę dzięki wielkie za poświęcony czas
Myślałem że już poszedłeś al mi zależało na tym
zadaniu.
*
Niech f(h) = −h4 + 100h2
Osiaga ona ekstrema dla tych samych argumentow co funkcja P(a).
*
To jest moment którego mi było trzeba . Własnie miałem problem z tą pochodną jak bym chciał to
liczyć pod schemat, bo generalnei zadanie było takie typowe.
Na prawdę dzięki wielkie za poświęcony czas 