trojkat rownoboczny 5-latek: Punkty Di E dziela boki AB i AC trojkata rownobocznego ABC w stosunkach |AD| : |DB|= |CE| : |EA|= 1 ; 2 Proste CD i BE przecinaja sie w punkcie O Udowodnij ze kąt AOB jest kątem prostym + do tego jakie woadomosci mam powtorzyc . dziekuje

Mila: Skąd masz to zadanie?

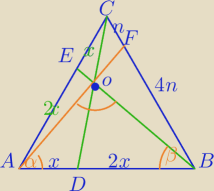
Mila: ΔCEB≡ΔCDA

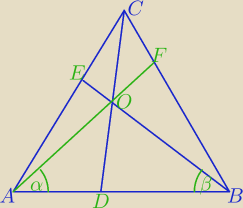
Rafal: Moje rozwiązanie (brzydkie, ale nic ładniejszego nie wymyśliłem). Kąty BAO i ABO to kąty ostre, zatem jeśli sinα=cosβ, to α=90−β. Z twierdzenia Leonarda Cevy http://www.deltami.edu.pl/temat/matematyka/geometria/planimetria/2011/02/01/Twierdzenie_Cevy/ (proste i użyteczne twierdzenie) widać, że |BF|=4|CF|, czyli

	4		1
|BF|=		a i |CF|=		a.
	5		5

	|BF|		|AF|		|BF|*sin60
Z twierdzenia sinusów w trójkącie BAF:		=		⇒sinα=		.
	sinα		sin60		|AF|

Z twierdzenia cosinusów w tym samy trójkącie:

	16		4		1		21		√21
|AF|2=a2+		a2−2*a*		a*		=...=		a2⇒|AF|=		.
	25		5		2		25		5

	4   √3   a* 5   2		2√7
Wracając do twierdzenia sinusów: sinα=		=...=		.
	√21   a 5		7

	√21
Podobnie (twierdzenie sinusów i cosinusów w trójkącie ABE): sinβ=		.
	7

Oczywiście sinα=cosβ, co kończy dowód.

5-latek: dziekuje za pomoc na razie to zadanie jest dla mnie za ciezkie ale wroce do niego .

Mila: Nie napisałeś na jakim poziomie to zadanie.

5-latek: Dobry wieczor Milu Poziom to 3 gimnazjum i 1 liceum . z tym ze to zadanie z kącika olimpijskiego Wiec na razie nie powinienem go tutaj pisac mam juz plana na nauke . Znalazlem ksiazke gdzie tresc jest podzielona na 49 lekcji (planimetrii dla samoukow .

5-latek: dzisiaj tak sie zastanawialem nad takim problemem czy linia srodkowa trapezu to jest ta linia ktora dzieli trapez na dwa wielokaty o rownych polach . Na razie sam nie potrafie na to pytanie odpowiedz

5-latek: Dobranoc Milu jutro rano do pracy muszse isc

Mila: Domyśliłam się ,że to zadanie konkursowe. Dobranoc. Mam rozwiązanie, ale chciałeś podpowiedzi. Rozwiązanie Rafała dobre.

Mila: Linia środkowa trapezu nie dzieli trapezu na trapezy o równych polach.

===: stosunkowo łatwo da się to policzyć tylko rachunkiem kątów ale skoro konkursowe ... to nie podpowiadam

Rafal: === Chętnie bym takie rozwiązanie zobaczył Mógłbyś podać link do zdjęcia rozwiązania (otworzy go tylko ten, kto będzie chciał).

5-latek: To nie jest zadanie z zadnego obecnego konkusu . To moze byc zadanie z 1976roku nawet .

5-latek: Mysle na razie nad tym. jesli nie zrobie to sie nic nie stanie .

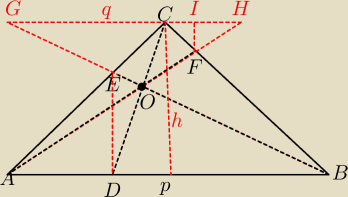
an: CF obliczamy z twierdzenia Cevy, Następnie z proporcji p i q Korzystamy z zależności w trójkącie prostokątnym h²=p*q (p+q=c), równość zachodzi a więc ∡AOC=90^o

===: ktoś tu pyta o kąt AOC