kombinatoryka Adamm: W klasie jest 15 dziewcząt i 16 chłopców. Spośród uczniów tej klasy tworzymy czteroosobową grupę. Na ile sposobów można to zrobić, tak aby w grupie były co najmniej 2 dziewczynki.

	15 2	16 2		15 3	16 1		15 4
zrobiłem to tak,			+			+		, co zgadza się z odpowiedzią

moje pytanie dotyczy czego innego, wcześniej próbowałem to rozwiązać tak najpierw wybieramy 2 osobową grupę z dziewczynek, a później dwuosobową grupę z reszty osób

	15 2	29 2
czyli			, moje pytanie jest o błąd w powyższym rozumowaniu, byłbym wdzięczny

gdyby ktoś mógł go wskazać i możliwie wytłumaczyć

Adamm:

Adamm:

Jerzy: Bo po wybraniu dwóch chłopców może sie zdarzyć,ze wybierzesz kolejnych dwóch kolejnych chłopcow.

Adamm: nie rozumiem jeśli wybiorę 2 dziewczynki, a potem 2 inne to i tak to jest spełnione przez warunek zadania

Natalia: Sądzę, ze to będzie tak: Co najmniej 2 dziewczynki, tzn. 2,3 lub 4 tak jak w poprawnym rozwiązaniu. Natomiast ty przyjąłeś że wybierzesz na pewno 2 dziewczynki i 2 osoby spośród 29. Czyli tymi dwoma osobami spośród 29 mogą być: jeden chłopiec i jedna dziewczynka co ostatecznie da ci 3 dziewczynki i jednego chłopca, więc obliczysz na ile sposobów możesz wybrać 3 dz i 1 ch. Obliczysz tak jakby jedną opcję z trzech (kiedy mogą być 3 dziewczynki), a musisz obliczyć jeszcze dwie dodatkowe opcje, kiedy będą 2 dziewczynki lub cztery.

yht: Niech 1,2,3,...,15 − dziewczynki a,b,c,...m,n,o,p − chłopcy

15 2
	− załóżmy że wybierzesz dziewczynki nr 1 i 2

29 2
	− wybierzesz dziewczynkę 3 i chłopca a

(1,2,3,a) − to twoja grupa ale równie dobrze może być tak:

15 2
	− wybierzesz dziewczynki 1 i 3

29 2
	− dziewczynka 2 i chłopiec a

masz taką samą grupę, a dwukrotnie ją liczysz

Adamm: dziękuję

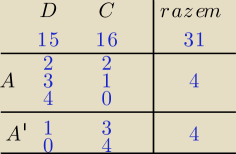
Bogdan: Zapis danych w postaci tabeli pozwala szybko ustalić odpowiedź. A − zdarzenie polegające na wybraniu 4−osobowej grupy, w której są co najmniej 2 dziewczynki, A' − zdarzenie przeciwne do A