Horner Metis: Wiedząc, że jednym z pierwiastków W(x)=z⁴−3z²+2z²+2z−4 jest z₀=1+1 znajdź pozostałe. Jak podzielić poprawnie Hornerem?

Jack: tak jak zawsze ?

Metis: z₀ = 1+i − mój błąd Nie wiem czy z zamieniać na x+iy do tego dzielić przez −1

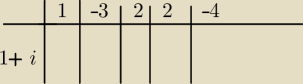
Jack: ja bym tak to zrobil.

jc: Wielomian ma współczynniki rzeczywiste, więc sprzężenie pierwiastka też będzie pierwiastkiem. Zatem wielomian (o ile autor zadania się nie pomylił) dzieli się przez wielomian (x−1−i)(x−1+i) = (x−1)² + 1 = x² − 2x + 2

Jack: ano prawda : D

Metis: No tak, zapomniałem o tym twierdzeniu, dzięki jc

Metis: Czyli u mnie zamiast x po prostu z ?

jc: W pamięci = (x²−2x+2)(x²−x−2)=(x²−2x+2)(x+1)(x−2), ale lepiej sprawdź

jc: z czy x, wszystko jedno. z ma przypominać, że mamy liczby zespolone.

Metis: !

PrzyszlyMakler: Respekt za dzielenie wielomianów 4 stopnia w pamięci..

Metis: jc jest niezły

Mila: W(x)=z⁴−3z³+2z²+2z−4 zgodnie z poleceniem: w(1)=1−3+2+2−4≠0 w(−1)=1+3+2−2−4=0 Schemat Hornera z=−1 1 −3 2 2 −4 1 −4 6 −4 0 z⁴−3z³+2z²+2z−4 =(z+1)*(z³−4z²+6z−4) P(x)=(z³−4z²+6z−4) P(−1)=−1−4−6−4≠0 P(2)=8−4*4+12−4=0 Schemat Hornera z=2 1 −4 6 −4 1 −2 2 0 ⇔(z+1)*(z³−4z²+6z−4)=(z+1)*(z+2)*(z²−2z+2) dalej sam.