Ciągłość funkcji pomóżcie BiednyStudent:

	⎧	ln(4−x)x−4, x<4
f(x)=	⎨	23, x=0
	⎩	16−x2x−4, x>4

a treść zadania to "Zbadaj ciągłosć funkcji f w punkcie x₀=0" Czy może mi ktoś wyjaśnić jak robić tego typu zadania?

Jerzy:

	2
Sprawdzić, czy granica funkcji (górnej) przy x →0+ jest równa
	3

Omikron: To nie jest funkcja, dla argumentu 0 przyjmuje dwie wartości.

BiednyStudent: Jak to przyjmuje 2 wartości dla zera?

Omikron:

2		ln4
	i
3		−4

Jerzy:

	2
f(0) =
	3

Adamm:

	ln(4−x)		ln4		2
pisze		dla x<4, zatem przyjmuje wartość		dla x=0 oraz		dla x=0
	x−4		−4		3

to jest funkcja wielowartościowa

BiednyStudent:

	e4
Granica "górnej funkcji" jest równa		tak?
	−4

Jerzy:

	ln4
Funkcja jest nieciągła w punkcie x = 0, bo w tym punkcie "wyrwano" jej wartość
	−4

	2
i zastąpiono wartoscią
	3

Adamm: nieprawda bo to nie jest funkcja

BiednyStudent: to jest zadanie z przykładowego kolokwium więc gyby mi się takie trafiło to co mam napisać?

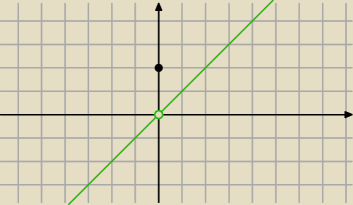
Jerzy: Z formalnego punktu widzenia ..nie jest, ale jeśli dobrze przepisana treść zadania, to można ją lekko "naciągnąć" Np: f(x) = x i f(x) = 2 dla x = 0

Jerzy: Sprawdź, czy dobrze przepisałeś przedział okresloności ( dziedziny) tej funkcji.

Jerzy: a powinno być: f(x) = x dla x ∊ (−∞,0) U (0,+∞) i f(x) = 2 dla x = 0

BiednyStudent: http://imgur.com/a/Vhyro

Jerzy: No jest dylemat, bo to faktycznie ( przy takim zapisie ) nie jest funkcja.

BiednyStudent: :(

Omikron:

	2
Myślę, że intencją autora było		dla x=4 i zbadać ciągłość w tym punkcie.
	3