algebra ww: algebra: Jeżeli v i u są niezerowymi wektorami oraz długość v=długość u. Oblicz kat między v−u i v+u.

	(v−u)*(v+u)
Myślałam, żeby skorzystać ze wzoru cosα=		Tylko nie wiem
	||v+u|| * ||v−u||

jak za bardzo to dokończyć

Adamm: v=<v_x; v_y> u=<u_x; u_y> spróbuj podstawić koordynaty, może coś się skróci

Adamm: v_x²+v_y²=u_x²+u_y²

	vx2−ux2+vy2−uy2
cosα =		= 0
	|v+u||v−u|

ww: a można od razu zakładać, że to wektory w przestrzni dwuwymiarowej?

Adamm: tak trudno to uogólnić?

Adamm: v=<v_x1;...; v_xn> u=<u_x1;...;u_xn> |v|=|u| ⇔ v_x1²+...+v_xn²=u_x1²+...+u_xn² (v−u)•(v+u)=v_x1²−u_x1²+...+v_xn²−u_xn²=0

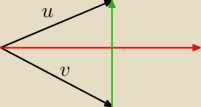
g: Jeśli u i v są tej samej długości, to (u+v) i (u−v) są prostopadłe.