| a2√2 | ||
Pomóżcie dojść do wyniku P= | ||
| 4 |
| a√3 | ||
h= | ||
| 2 |
| 1 | ||
H2+( | h)2 =h2
| |
| 3 |
| 1 | ||
H2 + | h2=h2
| |
| 9 |
| 8 | ||
H2= | h2
| |
| 9 |
| 2√2 | 2√2 | a√3 | a√6 | |||||
H= | h = | * | = | |||||
| 3 | 3 | 2 | 3 |
| 1 | a√6 | a√3 | 1 | a2√18 | a2*3√2 | |||||||
P=H*h * | = | * | * | = | = | =
| ||||||
| 2 | 3 | 2 | 2 | 12 | 12 |
| a2√2 | |
| 4 |
 a wytłumaczysz to wyliczanie H
a wytłumaczysz to wyliczanie H bo nie mogę troche dojść które boki wziąłeś...?
bo nie mogę troche dojść które boki wziąłeś...?

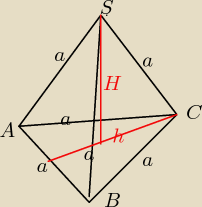
 w czworościanie foremnym wszystkie ściany są takie same czyli ich krawędzie i wysokości są
równe
spodek wysokości (S) pada na środek trójkąta równobocznego który dzieli wysokość w podanym
stosunku. i z twierdzenia potagorasa wyliczyłem wysokość to już dalej będizesz wiedział
w czworościanie foremnym wszystkie ściany są takie same czyli ich krawędzie i wysokości są
równe
spodek wysokości (S) pada na środek trójkąta równobocznego który dzieli wysokość w podanym
stosunku. i z twierdzenia potagorasa wyliczyłem wysokość to już dalej będizesz wiedział
 bo właśnie nie byłem pewny czy w takim czymś ta wysokość tak dzieli
bo właśnie nie byłem pewny czy w takim czymś ta wysokość tak dzieli  teraz już elegancko rozumiem
teraz już elegancko rozumiem dzięki za cierpliwość
dzięki za cierpliwość
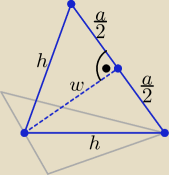 Można krócej i bez H:
Można krócej i bez H:
| a√3 | a | |||
h = | , w = √h2 − (a / 2)2 = √ (3a2 / 4) − (a2 / 4) = | √2 | ||
| 2 | 2 |
| a | a | a2√2 | ||||
P = | * | √2 = | ||||
| 2 | 2 | 4 |
| a√3 | a√3 | |||
trójkąta: | , | , a. | ||
| 2 | 2 |
| a2√2 | ||
P − pole omawianego przekroju, P = | ||
| 4 |
| 1 | ||
Objętość czworościanu foremnego V = | aP | |
| 3 |
| 1 | a2√2 | a3√2 | ||||
V = | a * | = | ||||
| 3 | 4 | 12 |