geometria analityczna 23: Dany jest trójkąt ABC o współrzędnych A(−4,1), B(−1,−3), C=(4,2). Napisz równanie prostej, w której zawiera się dwusieczna kąta ABC oraz wyznacz współrzędne takiego punktu D, że czworokąt o kolejnych wierzchołkach ABCD jest równoległobokiem.

23:

Paweł: https://matematykaszkolna.pl/strona/498.html spróbuj coś pokombinowac z tym twierdzeniem

===: chyba nie tak

===: 1. Napisz równanie prostej przechodzącej przez punkty A i B 2. Napisz równanie prostej przechodzącej przez punkty B i C Oba te równania do postaci ogólnej 3. Napisz równanie pęku prostych przez punkt C Szukaj na niej Punktu P równoodległego od prostych przez A i B oraz B i C

===: możesz też inaczej ...wyznaczając kąt ABC a dalej tangens kąta nachylenia dwusiecznej do 0x a potem już jej równanie

Eta: W sposobie podanym przez === (ale w tym zadaniu rachunki niezbyt przyjazne to: 2 sposób 1/ wyznaczamy współczynniki kierunkowe prostych :

	4
AB : a1=...= −		i BC : a2= ... = 1
	3

	|a1−a2|
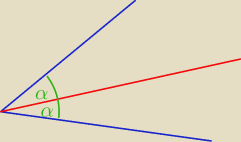
2/ tg2α =		= .... = −7
	1+a1*a2

	2tgα
3/ tgα=		= −7 ⇒ 7tg2α−2tgα−7=0 Δ=200 , √Δ=10√2
	1−tg2α

	1+5√2		1−5√2
tgα=		=a3 v tgα=		=a4
	7		7

dwusieczne mają równania: y= a₃(x−x_B)+y_B ⇒ y=............. lub y= a₄(x−x_B)+y_B ⇒ y=................

Eta:

===: Ecinka a cóż to za tg2α

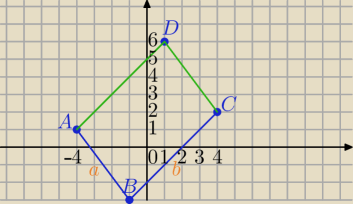
Mila: A(−4,1), B(−1,−3), C=(4,2) b) BC^→[5,5] A=(−4,1)→T_[5,5]→D=(−4+5,1+5)=(1,6) a) dwusieczna ∡ABC − każdy punkt dwusiecznej kąta jest jednakowo odległy od ramion kąta Prosta AB: y=ax+b 1=−4a+b −3=−a+b −−−−−−−−−−−odejmuję stronami

	4		13
4=−3a, a=−		, b=−
	3		3

	4		13
y=−		x−		⇔ a: 4x+3y+13=0
	3		3

b: y=x−2⇔x−y−2=0 S=(x',y') − punkt dwusiecznej

	|4x'+3y'+13|
d(S,a)=
	√42+32

	|x'−y'−2|
d(S,b)=
	√2

|4x'+3y'+13|		|x'−y'−2|
	=
5		√2

Dokończ

Eta:

===: tylko skąd te −7

Eta: w 3/ poprawiam zapis .................... ......................

	2tgα
tg2α=		= −7 ⇒
	1−tg2α

Eta: === Z 2/ .......... (policz

Eta: https://matematykaszkolna.pl/strona/1228.html zamiast Φ to 2α

Eta: φφφ η

===: to rozumiem ... ale przecież tam wszystko jest pod modułem ... mianownik też

Eta: A no tak.... racja .............

Eta: Nie dopisałam modułu w mianowniku i.......... poszło

Eta: tg(2α)=+7 to 7tg²α+2tgα−7=0 itd ........... Niech zainteresowany już sam to poprawi

===: .... poszło ... do lasu .... na "ducha puszczy"

===: a zainteresowany po 23:00 już poszedł lulu

Mila: b)

BA→		[−3,4]		−3		4
	=		=[		,		]
|BA|		5		5		5

BC→		[5,5]		1		1		√2		√2
	=		=[		,		]=[		,		]
|BC|		5√2		√2		√2		2		2

Wektory znormalizowane,

	−3		4		√2		√2
k→=[		,		]+[		,		]=
	5		5		2		2

	√2		3		√2		4		5√2−6		5√2+8
k→=[		−		,		+		] =[		,		]− wektor kierunkowy
	2		5		2		5		10		10

dwusiecznej B(−1,−3)

x+1		y+3
	=		⇔
5√2−6   10		5√2+8   10

x+1		y+3
	=
5√2−6		5√2+8

23: Jestem, tylko nie mam dostępu do komputera. dziękuję za pomoc