Stereometria
danek: Podstawą graniastosłupa prostego jest trójkąt ABC taki, że |AB| = 8, |BC| = 7, |AC| = 5.
Poprowadzono płaszczyznę prostopadłą do podstawy graniastosłupa i zawierającą wysokość
podstawy opuszczoną na najdłuższy bok trójkąta ABC. Pole otrzymanego przekroju jest równe 30.
Oblicz objętość graniastosłupa
Pomoże ktoś? proszę o pomoc...
12 sty 19:15
danek: jak to zrobić, prosze o pomoc
12 sty 20:03
danek: ktoś wie? podpowie?
12 sty 20:50
danek:
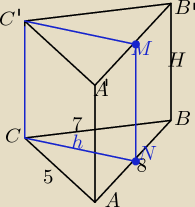
12 sty 22:08
danek: Jak to rozwiązać żeby objętość wyszła V=120
12 sty 22:11
Godzio: zaraz coś pokombinuje i skorzystam ze wzoru Herona żeby było łatwiej
13 sty 00:02
Godzio:
| | 1 | | 1 | |
p= |
| (a+b+c) = |
| *20 = 10
|
| | 2 | | 2 | |
P=
√p(p−a)(p−b)(p−c)=
√10*5*2*3 = 10
√3
20
√3=8h
30 = h*H
| | 2 | | 12√3 | |
H=30* |
| = |
| = 4√3
|
| | 5√3 | | 3 | |
V=Pp*H = 10
√3 * 4
√3 = 40*3 = 120
13 sty 00:05
Sabin:
Można też tak i chyba wszystko co nie ma wzoru Herona jest łatwiejsze

:
V = P
pH
P
p =
12|AB|h = 4h
z pola przekroju mamy że: hH = 30 czyli H =
30h
Stąd:
V = 4h *
30h = 120
13 sty 00:10
Godzio: też prawda

13 sty 00:41

 :
V = PpH
Pp = 12|AB|h = 4h
z pola przekroju mamy że: hH = 30 czyli H = 30h
Stąd:
V = 4h * 30h = 120
:
V = PpH
Pp = 12|AB|h = 4h
z pola przekroju mamy że: hH = 30 czyli H = 30h
Stąd:
V = 4h * 30h = 120
