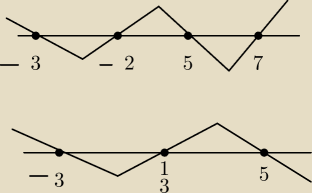
dd rejnold: Czy dobrze rozwiązałem nierówność?

	2x2−7x−29
1<		< 2
	x2−2x−15

D = R\{−3,5} 1 przypadek

2x2−7x−29
	>1
x2−2x−15

2x2−7x−29		x2−2x−15
	−		>0
x2−2x−15		x2−2x−15

x2−5x−14
	>0
x2−2x−15

(x²−5x−14)(x²−2x−15)>0 dla x²−5x−14 Δ= 25−4*(−14)=81 x₁ = −2 x₂ = 7 dla x²−2x−15 Δ=4−4*(−15)=64 x₁ = 5 x₂ = −3 x ∊ (−oo, −3) ∪ (−2,5) ∪ (7, +oo) −−−−−−−−−−−−−−−−−−−−−−−−−−−− 2 przypadek

2x2−7x−29
	<2
x2−2x−15

2x2−7x−29		2(x2−2x−15)
	−		<0
x2−2x−15		x2−2x−15

−3x+1
x2−2x−15

(−3x+1)(x²−2x−15) <0

	1
x=		, x=5, x=−3
	3

	1
x ∊ (−3,		) U (5,+oo)
	3

	1
Odp: x ∊ (−oo, −3) ∪ (−2,5) ∪ (7, +oo) u (−3,		) U (5,+oo)
	3

Dobrze zrobiłem?

rejnold:

rejnold: Sprawdzi ktoś? Mam z tego kartkóweczkę i muszę być pewny czy dobrze to zrobiłem/

Omikron: Na pewno zła odpowiedź nawet jeżeli obie nierówności są dobrze policzone. Przy podwójnej nierówności obie muszą być spełnione na raz. Szukasz więc części wspólnej rozwiązań.

rejnold: OBU ROZWIĄZAN NARAZ?

Omikron: Tak, pomiędzy dwoma nierównościami, które rozpatrujesz, jest koniunkcja.

tomek: dokładnie ... koniunkcja... zestaw otrzymane zbiory na osi liczbowej i wyznacz część wspólną

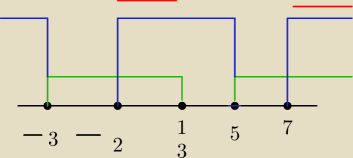
rejnold: czyli część wspólna , to x e (−2,1/3) u (7,+00)?

rejnold: No i tak wolfram pokazuje. Super dzięki