Badanie przebiegu zmienności funkcji st138: Zbadaj przebieg zmienności f(x) = √xlnx

Jerzy: Na początek: 1) Dziedzina 2) Pochodna i jej analiza

Jerzy:

	lnx		√x		lnx + 2√x
f'(x) =		+		=
	2x		x		2x

Jerzy:

	lnx		√x
f'(x) =		+		.... oczywiście.
	2√x		x

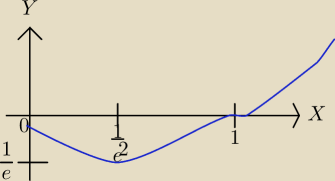st138: D_f = (0, ∞) f(x) = 0 ⇔ x=1 f−cja nie jest parzysta i nie jest nieparzysta Lim_x→∞ f(x) = ∞ Lim_x→0+ f(x) = 0 f−cja nie ma asymptot

	√x(lnx + 2)
f'(x) =
	2x

f'(x) = 0 ⇔ x=e⁻² f'(x)>0 ⇔ x∊(e⁻², ∞) f−cja rośnie f'(x)<0 ⇔ x∊(0, e⁻²) f−cja maleje

	−√xlnx
f''(x) =
	4x2

D_f'' = D_f' = D_f f''(x)=0 ⇔ x=1 f''(x)>0 ⇔ x∊(0,1) f''(x)<0 ⇔ x∊(1,∞) Punkt przegięcia f−cji: P=(1,0) i szkicuje wykres, dobrze?