Trygonometria
Mate: Przekształcenie funkcji trygonometrycznych.
Witam, jak narysować funkcję y = tg 3x?
Zrobiłem tak:
1) Narysowałem funkcję y = tg x
2) Wyznaczyłem miejsca zerowe funkcji y = tg 3x
3) zaznaczyłem na osi. I w tym momencie stanąłęm.
Nie wiem jak na podstawie tych miejsc zerowych rysować, mam na myśli to, że to "ramię" tangensa
wychodzi mi za duże. Jak to przeskalować?
6 gru 15:01
Macko z Bogdanca: tg3x czyli funkcja 3 razy sie ,,zwęża''
6 gru 15:03
Jerzy:
| | π | | π | |
Asymptoty: 3x = (2k + 1)* |
| ⇔ x = (2k+1)* |
| |
| | 2 | | 6 | |
reszta bez zmian.
6 gru 15:04
Jerzy:
Masz asymptoty co 30o ( pierwsza w 30o )
6 gru 15:05
Jerzy:
Ściślej ... w nieparzystch wielokrotnościach 30o
6 gru 15:07
Mate: W dalszym ciągu nie rozumiem, przepraszam..
6 gru 15:22
Jerzy:
Funkcja tgx ma asymptoty w nieparzystch wielokrotnościach kąta 90o
tg3x w nieparzystych wielokrotnościach kąta 30o
6 gru 15:24
Mate: Tak, to zrozumiałem. Jednak pozostałe punkty wykresu chyba też ulegają zmianie?
6 gru 15:28
Macko z Bogdanca:
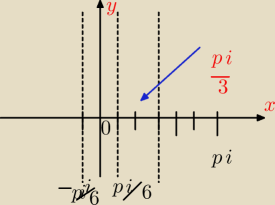
Narysuj sobie funkcje tangens w przedizale −pi/2,pi/2 Miejsce zerowe to 0 Natepnie −pi/2 i pi/2
podziel przez
3 bo o tyle zweza sie funkcja gdybys mial tg1/2x to wiadomo ze wydluzy sie 2 razy tak?
Otrzymasz wiec
funckje tangens w przedziale −pi/6,pi/6 miejscem zerowym takze bedzie 0, Dlaczego? Mozesz sobie
policzyc wartosc bezwgledna
−pi/6 oraz pi/6 To bedzie nasza ,,granica kolejnych przedizalow'' taka odleglosc... Otrzymasz
zatem 2pi/6, Jak wyskalujesz rzedna na 6 kresek
to bedzie to wygladalo tak, reszte rob analogicznie
6 gru 15:42
tomek:
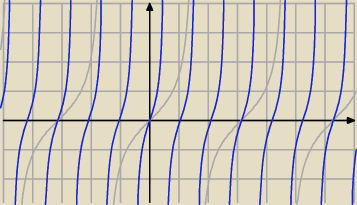
6 gru 15:49
 Narysuj sobie funkcje tangens w przedizale −pi/2,pi/2 Miejsce zerowe to 0 Natepnie −pi/2 i pi/2
podziel przez
3 bo o tyle zweza sie funkcja gdybys mial tg1/2x to wiadomo ze wydluzy sie 2 razy tak?
Otrzymasz wiec
funckje tangens w przedziale −pi/6,pi/6 miejscem zerowym takze bedzie 0, Dlaczego? Mozesz sobie
policzyc wartosc bezwgledna
−pi/6 oraz pi/6 To bedzie nasza ,,granica kolejnych przedizalow'' taka odleglosc... Otrzymasz
zatem 2pi/6, Jak wyskalujesz rzedna na 6 kresek
to bedzie to wygladalo tak, reszte rob analogicznie
Narysuj sobie funkcje tangens w przedizale −pi/2,pi/2 Miejsce zerowe to 0 Natepnie −pi/2 i pi/2
podziel przez
3 bo o tyle zweza sie funkcja gdybys mial tg1/2x to wiadomo ze wydluzy sie 2 razy tak?
Otrzymasz wiec
funckje tangens w przedziale −pi/6,pi/6 miejscem zerowym takze bedzie 0, Dlaczego? Mozesz sobie
policzyc wartosc bezwgledna
−pi/6 oraz pi/6 To bedzie nasza ,,granica kolejnych przedizalow'' taka odleglosc... Otrzymasz
zatem 2pi/6, Jak wyskalujesz rzedna na 6 kresek
to bedzie to wygladalo tak, reszte rob analogicznie
