| 2 | ||
Punkt p o dodatnich współrzędnych należy do wykresu funkcji określonej wzorem f(x)= | . | |
| x |
| 4 | ||
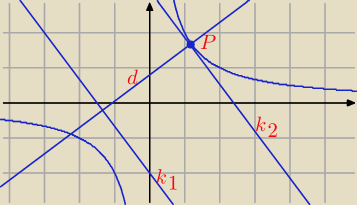
Wyznacz odciętą punktu P tak, aby jego odległość od prostej o równaniu y=− | x−2 była | |
| 3 |
| 4 | ||
k1: y = − | x − 2 ⇒ 4x + 3y + 6 = 0 | |
| 3 |
| 2 | ||
P = (x, | ) i x > 0 | |
| x |
| 4x2 + 6x + 6 | ||||||||||||
d = | = | ||||||||||||
| √16 + 9 | 5x |
| 4x2 + 6x + 6 | ||
d(x) = | → minimum itd | |
| 5x |
| 4 | 4 | |||
k2: y = a2x + b2, k2 ∥ k1 ⇒ a2 = − | , y = − | x + b2 | ||
| 3 | 3 |
| 2 | ||
Punkt P jest punktem jedynym wspólnym hiperboli y = | i prostej k2 | |
| x |
| 4 | 2 | |||
− | x + b2 = | ⇒ 4x2 − 3b2x + 6 = 0 i Δ = 0 itd. | ||
| 3 | x |
Pozdrawiam 
| 2 | ||
f(x)= | , x>0 | |
| x |
| −2 | ||
f'(x)= | ||
| x2 |
| −4 | ||
f'(x0)=a= | ||
| 3 |
| −2 | −4 | ||
= | |||
| x02 | 3 |
| 3 | ||
x02= | ∧ x0>0 | |
| 2 |
| 3 | √6 | |||
x0=√ | = | |||
| 2 | 2 |
| 2 | 4 | 2√6 | ||||
y0= | = | = | ||||
| x0 | √6 | 3 |
| −4 | ||
y= | x−2 |*(−3) | |
| 3 |
| |4x0+3y+6| | 6+4√6 | |||
d(P,l)= | = | |||
| √42+32 | 5 |