Stereometria danek: Kąt dwuścienny między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego jest równy 120 stopni. Wyznacz stosunek krawędzi bocznej do krawędzi podstawy ostrosłupa. Pomoże ktoś? proszę o pomoc...

danek: wiecie co z tym zrobić?

danek: ktoś wie? podpowie?

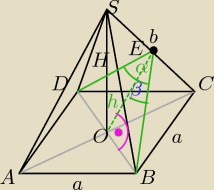
danek: α=120 stopni β=U[1]{2}α=60 stopni

danek: za to zadanko jest aż 7 punktów... pomoże ktoś?

danek:

	b		√3
a wynik powinien wyjść		=
	a		2

danek: dwuścienny jest zaznaczony α

danek: to kąt pomiędzy ścianami bocznymi

Godzio: wiem co to już jest, a może ma jakieś zależności że dzili b na 2 równe części alebo pada pod kątem prostym na "b" bo tak to nie zabardzo moge obliczyć można tylko wywnioskować że

	1
h√3 =		d
	2

	a√2
h√3 =
	2

h√6 = a

danek: no nie, powiem Ci że nie dzieli w żaden sposób b na pewno

danek: ale widzę że możemy tutaj zrobić TW.COS i od tego zacząć

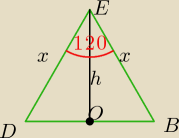
danek: możena tak z tego zrobić żczy to będzie złe?

Godzio: niestety jeszcze nie przerabiałem twierdzenia cosinusów także w tym zadaniu chyba Ci nie pomoge ale na pewno ktoś to zrobi ja już lece spać

danek: aha no dzięki Ci wielkie za pomoc w każdym razie, dobrej nocy

danek: w podstawie jest kwasrat zatem przekątna ma a√2

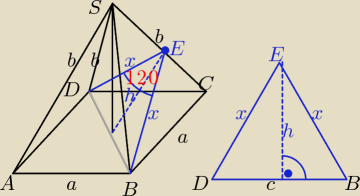
danek: c jest tutaj przekątną podstawy (kwadrat) i jest równa a√2 teraz wykorzystuje TWIERDZENIE COSINUSÓW (a√2)²=x²+x²−2*x*x*cos120^◯ 2a²=2x²−2x²(cos(90+30) =2x²−2x²(−sin30)

	1
=2x2−2x2(−		)
	2

2a²=3x²

	2a2
x2=
	3

	a√6
x=
	3

danek: ale co teraz? żeby wyznaczyć b? jaki układ równań?

Bogdan:

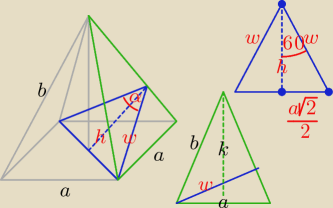
a√2   2		a√2   2		√3		a√2
	= sin60o ⇒		=		⇒ w =
w		w		2		√3

k = √b² − (a / 2)²

1		1		b		k
	bw =		ak ⇒		=		⇒
2		2		a		w

	b		√b2 − (a / 2)2
⇒		=
	a		a√2     √3

po obustronnym podniesieniu do kwadratu i uproszczeniu otrzymujemy:

2		a2		b2		a2		b2		3
	b2 = b2 −		⇒		=		⇒		=
3		4		3		4		a2		4

	b		√3
Stąd		=
	a		2

danek: ale fajnie , dzięki Bogdan a spojrzysz na to? https://matematykaszkolna.pl/forum/33891.html