funkcje bartek: Proszę kogoś o dokładne wytłumaczenie tego typu zadań wyznacz liczbe a, dla której dziedziną funkcji f jest podany obok wzoru funkcji zbiór Df

	2x
f(x)=		Df=R\{−5,−2}
	(x−a)(x+5)

Adamm: x−a≠0 ∧ x+5≠0 ⇔ x≠a ∧ x≠−5 hmmm, co może być liczbą "a" no bo chyba nie −2, prawda?

bartek: kompletnie tego nie rozumiem, bo w odpowiedziach jest −2 a x przecież może być równe −2, a więc dlaczego x≠a ?

Natalia: Żeby można było obliczyć jakikolwiek ułamek, w mianowniku nie może być zero, ponieważ dzielenie przez zero jest niewykonalne. Dlatego mianownik nie może się zerowac. Takie wyrażenie (x−a)(x+5) zeruje się, gdy jedna z liczb jest zerem. Dlatego a=2, tzn. że x≠−2 oraz x≠−5.

bartek: ale a może być też np. 10 i również się nie wyzeruje

Natalia: Sorry tam powinno być, że a=−2. Do dziedziny należą liczby,które moga spełniać równanie. Czyli w tym przypadku wszystkie liczby rzeczywiste oprócz (−5) i (−2), które zerują mianownik.

bartek: coś się rozjaśnia, ale dalej pewności nie mam. dlatego prosiłbym jeszcze o wytłumaczenie jednego przykładu i wtedy dokładnie wszystko przeanalizuje

	1
f(x)=		Df=(−∞,1)
	√3a−x

Natalia: Mianownik nie może być zerem i jednocześnie wyrażenie pod pierwiastkiem nie jest ujemne, czyli D: 3a−x >0

	1
3a>x. Wiemy, że x<1, czyli 3a=1 a=
	3

bartek: Jednak nadal nie rozumiem

Natalia: Coś pod pierwiastkiem nie może być ujemne. Nie można wykonać takiego działania √−4. Natomiast można √4. Dlatego coś pod pierwiastkiem może być ≥0. √0=0. Ale ponieważ to jest mianownik to w mianowniku nie może być zero czyli to co jest pod pierwiastkiem musi być >0 (bo zerem być nie może bo to mianownik). Dlatego 3a−x>0 3a>x, wiem że D_f=(−∞;1) czyli x<1, czyli 1>x

	1
Więc 3a musi być równe 1, czyli a=		.
	3

bartek: to wcześniej wszystko rozumiem, tylko dlaczego 3a musi być równe 1 ? przecież do dziedziny nie należy 1

bartek: Naprawdę chciałbym to ogarnąć

Natalia: Porównujesz nierówności 3a>x i 1>x. W nierówności z "a" chcesz żeby twój "x" był mniejszy od 1 czyli szukasz "a" dla którego 3a=1.

bartek: a np takie:

	1
f(x)=√x+4+		Df=<−4,1)u(1,+∞)
	x+a

to już ostatni przykład, jeśli po tym nie ogarnę to znaczy że nie dane mi to umieć

Natalia: Jakie byś postawił warunki?

bartek: x+4≥0 i x+a≠0 Czyli x≥−4 i x≠−a I dalej nie wiem

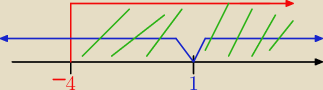
Natalia: Twoja dziedzina wygląda tak jak wyżej. Obliczyłeś już x≥−4, czyli potrzebujesz jeszcze takiego warunku, który w którym x ∊ R−{1}. Do oblicznia został ci warunek x≠−a. Czyli 1=−a ; a=−1.

bartek: Dziękuję serdecznie na poświęcony czas

Natalia: