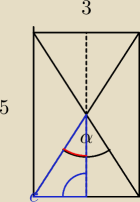
Oblicz sinus kąta stworzonego przez przekątne w prostokącie - gdzie mam błąd? Noomi: Długości boków prostokąta są równe 3 oraz 5. Oblicz sinus kąta ostrego, który tworzą przekątne tego prostokąta. Zrobiłam tak, że zajęłam się najpierw tym niebieskim trójkątem. Wyszło mi z niego, że sinus czerwonego kąta = 0,6, więc czerwony kąt = 37 Kąt α = 0,5 czerwonego kąta, więc = 74 stopnie sinus 74 stopni = 0,96. Ale według odpowiedzi ma wyjść 0,88. Gdzie mam błąd?

Jerzy: Moim zdaniem masz dobrze ... ( niepotrzbnie liczyłaś kąt ) sin(α/2) = 0,6 cos(α/2) = 0,8 sinα = 2sin(α/2)cos(α/2) = 2*0,6*0,8 = 0,96.

hehehe: nie liczy sie zamieniajac stopni na wartosc i potem z powrotem.

	3
wyszlo ci, ze sinus czerwonego =
	5

(jak?)

	3   2		3
najlatwiej obliczyc tangens czerwonego =		=		= 0,6
	5   2		5

a to nie jest sinus

sin x		3
	=
cos x		5

	3
sinx =		cosx
	5

z jedynki tryg. sin²x + cos²x =1

9
	cos2x + cos2x = 1
25

34
	cos2x = 1
25

	25
cos2x =
	34

	5
cosx =
	√34

sin²x = 1 − cos²x

	25		9
sin2x = 1 −		=
	34		34

	3
sinx =
	√34

sin2alfa to szukany kat.

	8
sin2alfa = 2sinalfa cosalfa = ... =
	√34

WISH u luck my friend pozdr,.,.

Jerzy: sin(α/2) = 0,6 ( jak ?) , prosto: d = √(1,5)² + (2,5)² = √6,25 = 2,5 sin(α/2) = (1/2):(2,5) = 0,6

hehehe: oczywiscie jeszcze razy 2 wynik

Jerzy: Teraz widzę błąd u mnie

Noomi: no już widzę, policzyłam tangens a zapisałam sinus. Ale wynikiem nie może być 8 podzielić na pierwiastek z 34 bo według CKE odpowiedź to 0,88...

Noomi: i w sumie dlaczego nie można zamieniać stopni na wartość skoro tak jest tysiąc razy szybciej? chodzi o to że to mniej dokładne czy w ogóle nie można bo to z jakiegoś powodu całkiem błędne?

Jerzy: Mniej dokładne.

Noomi: Jak już widzę że to tgβ = 0,6, a nie sinβ jak wcześniej napisałam, to tgβ = 0,6 => β= 31 st α = 2β = 62 st sin62 st = 0,88 skoro to wyszło i musiałam zapisać tylko 3 linijki zamiast całej strony to dlaczego tak nie można? życie byłoby łatwiejsze

Noomi: Aaa, ok, dziękuję Jerzy a nie orientujesz się może czy gdybym tak zrobiła na maturze to czy miałabym max punktów jeśli wynik jest zgodny z kluczem?

Jerzy: Akurat w tym przykładzie kąt jest dokładny.