prawdopodobienstwo warunkowe kebab: 20% uczniów czyta czasopismo motoryzacyjne 30% uczniów czyta czasopismo kobiece 40% uczniów czyta czasopismo młodzieżowe 13% uczniów czyta czasopismo motoryzacyjne i młodzieżowe 5% uczniów czyta czasopismo motoryzacyjne i kobiece 10% uczniów czyta czasopismo kobiece i młodzieżowe 5% uczniów czyta wszystkie trzy Oblicz prawdopodobienstwo tego ze losowo wybrany uczen nie czyta czasopism kobiecych, jesli czyta przynajmniej dwa rodzaje czasopism

tomek: diagram Venna do tego?

kebab: nie ma nic w poleceniu, ale możesz jak chcesz

tomek:

8
	...to dobra odpowiedź?
18

kebab: tak, ale poproszę o rozpisanie

kebab: i najlepiej wyjaśnienie czmu mianownik jest taki rozbudowany :

kebab: help

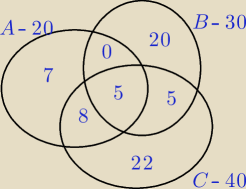
Bogdan: a może taki obrazek pomoże?

kebab: Wiem, że wyjdzie 8/18 i owszem bardzo pomoże, ale czy na maturze obrazek mi zaliczą? Czy obliczenia P(B'|(A n C) u (A n B) u (B n C))?

Bogdan: Obrazek jest tylko ilustracją, trzeba przedstawić analityczne uzasadnienie

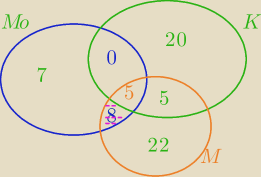
Mila: B− uczeń czyta przynajmniej dwa rodzaje czasopism |B|=5+5+8=18

	8		4
P(∼K/B)=		=
	18		9

kebab:

	P(AnB)
nie wiem jak to podstawić do wzoru P(A|B) =
	P(B)

P(B'|(A n C) u (A n B) u (B n C) − 2P (AnBnC) ) jak tak zrobie to potem za trudne się wydaje a jak instyktownie to robie to mi tak wychodzi i po przeliczzeniu dobry wynik

P(AnC) − (AnBnC)
P(A n C) u P(A n B) u P(B n C) − 2P (AnBnC)

czyli nie zawsze pod ten wzór trzeba podstawiać, tylko samemu wykombinować, tak logicznie pomyśleć?

kebab: Dziękuje Mila

kebab: Ale czy na maturze takie coś zaliczą? czy trzeba to rozpisać tym wzorem P(A|B)

Mila: Zaliczą. Nie przejmuj się tym zadaniem. Maturzyści od 2009 roku go rozwiązują. Postaram się pomyśleć nad innym wyjaśnieniem.