Proszę o sprwdzenia zadań z ekstremów i monotoniczności funkcji basia: Czy chciałby ktoś sprawdzić mi moje zadania z monotoniczności i ekstremów funkcji , (póki co określiłam tylko monotoniczność dla podanych funkcji) nie określałam jeszcze wartości w ekstremach. To co jest na czerwono napisane do udzielonych przeze mnie odpowiedzi to poprawne odpowiedzi z tyłu książki , natomiast funkcje zakreśliłam na pomarańczowo w kółkach http://www.fotosik.pl/zdjecie/bb9160baa5f924c7 http://www.fotosik.pl/zdjecie/6fc2db7f6bea17e5

basia: chciałabym aby ktoś mi wyjasnił co robię zle

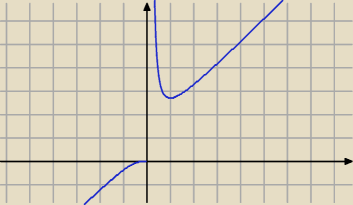
Janek191: Patrz na wykres funkcji f

Janek191: f rośnie w : ( − ∞ , 0), ( 1, +∞) f maleje w ( 0 , 1) f osiąga minimum lokalne w x = 1.

basia: no dobrze ale z miejsc zerowych nie otrzymuję przeciez 0 tylko ono nie nalezy do dziedziny i jak rysuje taki wykres to przechodzi mi też przez 0? pogubiłam się już , przyznaję że uczyłam się z etrapeza

Janek191: 0 nie należy do dziedziny. Tam są otwarte przedziały .

basia: jeśli mówimy o tym wykresie co narysowałam to powinna byc parabola skierowana ramionami do góry ?przechodząca przez 0 i 1?

basia: z tym że 0 odpada bo nie należy do dziedziny , mozna tak to narysiwać?

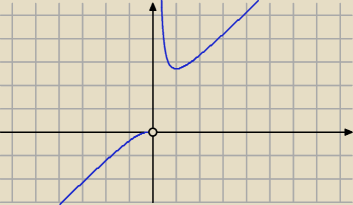
Janek191: f(x) = x*e^1_x x ≠ 0

	e1x		1
f '(x) = e1x −		= e1x*( 1 −		) = 0 ⇔ x = 1
	x		x

Dla x < 0 jest f '(x) > 0 więc f rośnie Dla x ∊ ( 0, 1) jest f '(x) < 0, więc f maleje Dla x > 1 jest f' (x) > 0, więc f rośnie

Janek191:

basia: no ok a 2 przykładzie dlaczego tam gdzie funkcja maleje pojawia się 1 jak nie otrzymałam jej w rozwiązaniach równania skąd ona się tam wzięła?

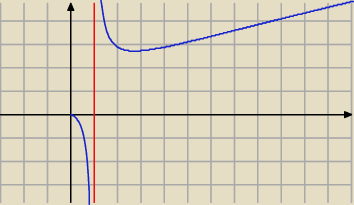
Janek191: f(x) = U{x}[ ln x} x > 0 i x ≠ 1

	ln x − 1
f '(x) =		= 0 ⇒ x = e
	ln2 x

Dla x ∊ ( 0, 1) jest f '(x) < 0, więc f maleje Dla x ∊ (1 , e) jest f '(x) < 0 , więc f maleje Dla x > e jest f '(x) > 0 , więc f rośnie Asymptota pinowa ma równanie x = 1

basia: w końcu już rozumiem dziekuję Ci jeszcze raz bardzo!

Janek191: x = 1 nie należy do dziedziny, bo ln 1 = 0 , a dzielenie przez 0 nie jest dozwolone.

basia: wiem wiem teraz się kapnęłam