Zadanie nr 54
Pumba57: Udowodnij ze dlugosc lamamnej zwyczajnej A1,A2 A3 A4 A5 jest wieksza od dlugosci odcinka
A1A5
czy podobna wlasnosc przysluguje kazdej lamanej zwyczajnej ?
Wypowiedz ogolne twierdzenie
4 gru 15:12
Pumba57:
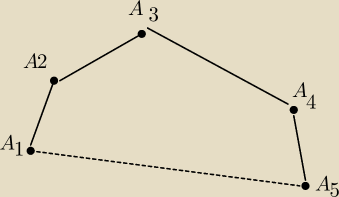
4 gru 15:24
Benny: Może indukcyjnie?
Mamy łamaną A1, A2, ..., An
Dla n=3 mamy nierówność trójkąta
|A1A2|+|A2A3|≤|A1A3|
Załóżmy, że działa dla pewnego n0=k
|A1A2|+|A2A3|+...+|Ak−1Ak|≤|A1Ak|
Udowodnimy, że działa dla n>n0
|A1A2|+|A2A3|+...+|Ak−1Ak|+|AkAk+1|≤ (z założenia indukcyjnego)
≤|A1Ak|+|AkAk+1|≤ (z nierówności trójkąta) |A1Ak+1|
4 gru 15:31
Pumba57: Benny 1 klasa liceum .
Ale za to dziekuje
4 gru 15:38
Benny: Tam zwroty powinny być w drugą stronę

4 gru 15:41
Pumba57: Tak zauwazylem (ale nie podnosilem larum

4 gru 15:42
Pumba57:
4 gru 16:23
Pumba57: jednak prosze o pomoc w tym zadaniu i nastepnym
4 gru 17:42
Saizou :
Tak jak napisał Benny wszystko sprowadza się do nierówności trójkąta.
tzn.
|A1A3| ≤ |A1A2|+|A2A2|
Potem rozważasz trójkąt A1A3A4 i korzystając z nierówności
|A1A4| ≤ |A1A3|+|A3A4| ≤|A1A2|+|A2A3|+|A3A4|
w kolejnym kroku wykonujesz to samo tylko dla trójkąta A1A4A5
i otrzymujesz tezę
4 gru 17:49
Pumba57: Na razie Saizou dziekuje .
4 gru 17:51
Pumba57: czyli \rozpatrujac trojkat A1A4A5 mamy
|A1A5|<|a1A4|+|A4A5| <|A1A2|+|A2A3|+|A3A4|+|A4A5|
==========================================================
4 gru 18:26


