czy funkcja ma ekstrema lokalne
OLa123: Mam zbadać czy funkcja: 3x4−4x3−6x2+12x+4 posiada ekstrema lokalne.
A więc w tym celu przyrównałam do zera otrzymana wcześniej pochodną i mam: że pochodna to(po
wciągnięciu przed
nawias):12(x3−x2−x+1)
Po przyrównaniu do zera mam dwa miejsca zerowe −1 i 1 . Wyszło mi że mam funkcja ma 1 ekstremum
min.
w punkcie −1 i wartośc ta −7 a na zajęciach wartośc ta (mam w zeszycie że wynosi 0) i teraz
pytanie czy pomylił się ćwiczeniowca
czy może ja , podejrzewam że on wziął −1 i podstawił do otrzymanej pochodnej i wyszło mu stąd
0?
4 gru 13:46
===:
źle policzona pochodna (albo błąd w zapisie funkcji) masz tam −12x czy +12x?
4 gru 13:58
OLa123: pochodna to: 12x3−12x2−12x+12=12(x3−x2−x+1) to gdzie jest błąd?
4 gru 14:16
OLa123: w funkcji mam +12x dlatego w pochodnej zostaje mi 12 i wyciągnęłam przed nawias 12 a w nawiasie
pozostało mi +1
4 gru 14:17
===:
przepraszam ... niedowidzę

4 gru 14:19
OLa123: nic się nie dzieje , każdemu się zdarza

a propo Twoim zdaniem ja się walnęłam czy
ćwiczeniowca ? xd
4 gru 14:21
===:
"zerując" pochodną dostajesz dwa pierwiastki z tym, że x=1 jest dwukrotnym.
Zatem dla x=1 masz nie ekstremum a punkt przegięcia

4 gru 14:24
OLa123: nie doszliśmy jeszcze na zajęciach do punktów przegięcia,nawet nie liczyliśmy2 pochodnej , mam
tylko w tabelce zapisane że dla 1 f(x) jak i f'(x) wartośc wynosi 0 ale skąd bo nie rozumiem
skąd się to wzięło

4 gru 14:27
===:
nie istotne ... rozwiąż porządnie f'(x)=0
4 gru 14:32
OLa123: wyszło mi że x=1 Który jest pierwiastkiem 2−krotnym i x=−1
4 gru 14:34
===:
zauważysz łatwo, że jednym z pierwiastków jest x=1 zatem dziel przez (x−1)
x2−1
(x3−x2−x+1):(x−1)
−x3+x2
−x+1
x−1
zatem x3−x2−x+1=(x−1)(x−1)(x+1)
4 gru 14:37
===:
skoro dwukrotnym to nie spełnia drugiego warunku dla ekstremum ... pochodna nie
zmienia znaku przy przejściu przez ten punkt
4 gru 14:38
OLa123: no to tak zgadza się tak otrzymałam

, tylko nie czaję skąd po podstawieniu do "funkcji" 1
otrzymana wartość wynosi 0
4 gru 14:41
OLa123: no ok ale −1 spełnia i jest ekstremum min. i wartość dla niej też mam 0 , jeśli −1 podstawie do
funkcji
4 gru 14:42
OLa123: nie powinno być −7?
4 gru 14:43
===:
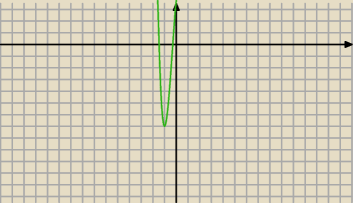
−7
4 gru 14:55
OLa123: ok dziękuje Ci bardzo w końcu mam już pewność

4 gru 15:05

 a propo Twoim zdaniem ja się walnęłam czy
ćwiczeniowca ? xd
a propo Twoim zdaniem ja się walnęłam czy
ćwiczeniowca ? xd


 , tylko nie czaję skąd po podstawieniu do "funkcji" 1
otrzymana wartość wynosi 0
, tylko nie czaję skąd po podstawieniu do "funkcji" 1
otrzymana wartość wynosi 0
 −7
−7
