Dla jakich wartości parametru a zbiór rozwiązań nierówności jest zawarty w... Iksik: Dla jakich wartości parametru a zbiór rozwiązań nierówności 2x − 3x + 2 < 0 jest zawarty w zbiorze rozwiązań nierówności ax² − (3a+ 1)x + 3 > 0 ? Wyliczyłem pierwszą nierówności i wychodzi na to, że x ∊ (1;2), czyli druga nierówność musi zahaczać o ten przedział. Przy a = 0 będzie x < 3 czyli zgadza się ze zbiorem Teraz proszę o pomoc przy równaniu kwadratowym, wiem, że będzie dużo warunków, które zależą od współczynnika a i Δ.

Iksik: Odświeżam

Iksik: Ponownie przyklejam żeby było widoczne w gąszczu wiadomości

Iksik: Nikt nie wie?

wojtek: Podbijam temat i od razu zapytam czy takie konkretne zadanie mogłoby się pojawić na maturze? Trochę jest zagmatwane, a z tego co patrzyłem, to w arkuszach są nieco łatwiejsze. Fajnie jakby ktoś narysował to na układzie współrzędnych.

Dominik: mogloby. nie wykracza poza material licealny.

konda: Pierwsze rownanie ma zapewne postac x² − 3x + 2 < 0 ?

wojtek: Tak, ma taką postać. Rozwiąże ktoś? Patrzyłem na rozwiązanie na konkurencyjnym(?) forum, i trochę niejasne jest dla mnie. Dla a>0 rozważali przypadek kiedy parabola będzie nad osią (Δ<0) i nie wiem dlaczego. Przecież wtedy ten przedział (1;2) nie będzie się zawierał w zbiorze rozwiązań drugiej nierówności?

konda: ax² − (3a+ 1)x + 3 > 0 Po mojemu to tak: a<0 Δ>0 I wzory Viete'a:

−b
	=3
a

c
	=2
a

wojtek: Dla a<0 kumam, a a>0? Zrób to ktoś, please

konda: http://www.zadania.info/d568/7379946 Też nie czaje tego

wojtek: No to jest gruba zagwozdka, a na grubą zagwozdkę przydałaby się jakaś gruba ryba tutaj z forum. Zapraszamy!

pigor: ... , widzę to np. tak : niech f(x)=ax²−(3a+1)x+3, to warunki zadania spełnia układ (koniunkcja) 4−ech nierówności : Δ_f>0 i a f(1) 0 i a f(2)<0 i 1< x_wf<2 ⇔ ⇔ (3a+1)²−12a >0 i a(a−3a−1+3)< 0 i a(4a−6a−2+3)< 0 i 1< ^3a+1_2a< 2 ⇔ ⇔ 9a²+6a+1−12a >0 i a(−2a+2)< 0 i a(−2a+1)< 0 i 2a²< a(3a+1) < 4a² ⇔ ⇔ 9a²−6a+1 >0 i a(a−1) >0 i a(a−¹₂) >0 i 2a²−3a²−a< 0 i 4a²−3a²−a >0 ⇔ ⇔ (3a−1)² >0 i (a<0 ∨ a>1) i (a<0 ∨ a >¹₂) i a²+a >0 i a²−a >0 ⇔ ⇔ 3a−1≠0 i (a<0 a>1) i a(a+1) >0 ⇔ a≠¹₃ i (a<0 ∨ a>1) i (a<−1 ∨ a >0) ⇔ ⇔ x<−1 ∨ 0< x< ¹₃ ∨ x>1 ⇔ x∊(−∞;−1) U (0;¹₃) U (1;+∞) . ...

pigor: .. , ale głowy sobie nie dam uciąć za to moje rozwiązanie , bo coś mi ...

wojtek: Ooo panie, to żeś pan pocisnął Odpowiedź jakby co to (−∞;0.5). Nie za bardzo rozumiem czemu wierzchołek musi być w przedziale (1;2), przecież jak parabola będzie odpowiednio szeroka, to x_w może mieć zupełnie inną wartość? Mógłby ktoś wykres machnąć?

wojtek: Bump. Myślę nad tym i im bardziej myślę, tym bardziej tego nie rozumiem. Zaraz zacznę się chyba cofać w rozwoju w ogóle.

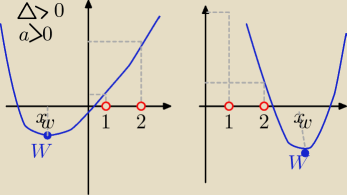
Eta: dla Δ≥0 f(1)>0 i f(2)>0 i x_w≤1 lub x_w≥2

wojtek: Wychodzi na to, że w ogóle polecenia nie zrozumiałem. Myślałem, że parabole mają "obejmować" przedział (1;2) Tzn widzę, że idąc ramionami w dół obejmuje ten przedział, więc czemu ramionami w górę ma go omijać?

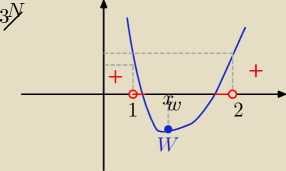
Eta: Na 3/ rysunku kontrprzykład Δ>0 i f(1)>0 i f(2)>0 ale x_w€(1,2) widzisz chyba,że zbiór rozwiązań f(x) >0 nie zawiera całego przedziału (1,2) Jasne?

wojtek: Na trzecim rysunku gdyby wierzchołek był ileś jednostek niżej, to by zawierał. Czemu nie może tak?

Eta: Cały przedział będzie się zawierał w zbiorze rozwiązań tej nierówności⇔ gdy będzie po lewej lub po prawej stronie od ramienia paraboli

wojtek: Jakie chore. Boże/Allahu/Jahwe/whatever ustrzeż mnie przed takim zadaniem na maturze, amen. Dzięki skarpEta!

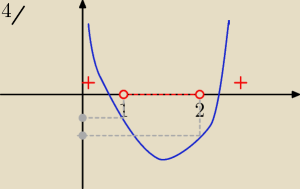
Eta: 4/ kontrprzykład Wtedy f(1) <0 i f(2)<0 i przedział (1,2) ⊄ w zbiorze rozwiązań nierówności f(x) >0 +