Geometria analityczna 3D pepe: 1. Znaleźć równanie płaszczyzny w postaci ogólnej zawierającej prostą l :

x − 2		z + 1
	= y − 3 =
2		4

i prostopadłej do płaszczyzny π : x − 2y − 3z + 7 = 0. 2. Znaleźć równanie płaszczyzny zawierającej prostą l₁ :

x − 1		z + 1
	= y + 2 =
3		−2

i równoległej do prostej l₂ :

⎧	x = −t − 2
⎨	y = 5t
⎩	z = t + 1

t ∈ R Bardzo proszę o pomoc przynajmniej z jednym z nich, na nic nie mogę wpaść. Z góry dziękuję!

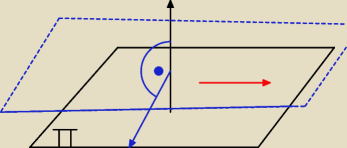
Jack: 1. (Nie gwarantuje ze to poprawne rozumowanie) Prosta l ma wektor (nazwimy go v) −−−> v = [2,0,4] oraz jakis punkt, nazwijmy go P(2,3,−1) Skoro mamy znalezc rownanie plaszczyzny, to potrzebujemy jakis punkt do niej nalezacy, no i to jest wlasnie nasze P(2,3,−1) potrzebujemy jeszcze wektor normalny. Plaszyzna π : x − 2y − 3z + 7 = 0 tzn, ze wektor prostopadly (normalny) do plaszczyzny, nazwijmy go n : n=[1,−2,−3] wektor prostopadly do wektora n oraz prostopadly rownoczesnie do v to wektor szukany. Wektory n i v sa rownolegle, zatem taki wektor znajdziemy poprzez iloczyn wektorowy wektorow v i n. zatem [2,0,4] x [1,−2,−3] = ... = [8,−10,−4] zatem szukane rownanie plaszczyzny to rownanie ogolne to Ax + By + Cz + D = 0 gdzie u nas P(2,3,−1) (czyli x = 2, y = 3, z = −1) oraz wektor [8,−10,−4] czyli A = 8, B = − 10, C = − 4 podstawiajac wszystko 8*2 − 3*10 + 4 + D = 0 D = 10 zatem rownanie tej plaszczyzny to 8x − 10y − 4z + 10 = 0 podzielmy sobie przez 2 4x − 5y − 2z + 5 = 0 PS nie masz moze odpowiedzi?